Homework 2 (Due: February 12)

[PDF]

Reading

Madhow: Appendix A, especially section A.3, and Section 3.1.

Problems

1. Madhow: Problem 3.2
2. Madhow: Problem 3.4
3. Let X and Y be independent Gaussian random variables with mean m = 0 and variance σ² = 1.
   1. Sketch a two-dimensional coordinate system with axes X and Y . Indicate the region R₁ = {X > α and Y > α} in that coordinate system; assume that α ≥ 0.
   2. Show that Pr{X > α,Y > α} = Q²(α). Note that this is the probability that a point (X,Y ) falls in the region R₁.
   3. Now, add the region R₂ = {X,Y ≥ 0 and X² + Y ² > 2α²} to your diagram. How does the region R₂ compare to R₁ from part (a)?
   4. Show that Pr{X,Y ≥ 0,X² +Y ² > 2α²} = 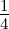exp(-α²). Note that this is the probability that a point (X,Y ) falls in the region R₂.
   5. From the above, show that we can conclude the well known bound

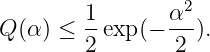
4. Let 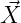be a zero mean Gaussian random vector with covariance matrix K.
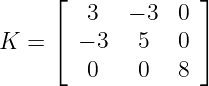
   1. Give an expression for the density function f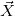(x).
   2. If Y = X₁ + 2X₂ - X₃, find f_Y (y).
   3. If the vector 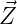has components defined by

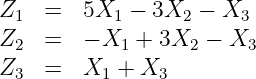
      determine f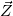(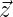). What are the properties of the new random vector?

   4. Determine f_X1|X2(x₁|x₂ = β)