Homework 1 (Due: January 29)

[PDF]

Reading

Madhow: Appendix A and Section 3.1.

Note: the material in sections A.1 and A.2 has been covered in ECE 528 and you are expected to be familiar and comfortable with that material.

Problems

These problems are review problems for probability and random variables.

1. A noisy discrete communication channel is available. Once each second one letter from the three-letter alphabet {a,b,c} can be transmitted and one letter from the three-letter alphabet {1, 2, 3} is received. The conditional probabilities of the various received letters, given the various transmitted letters are specified by the diagram in the accompanying diagram.

   

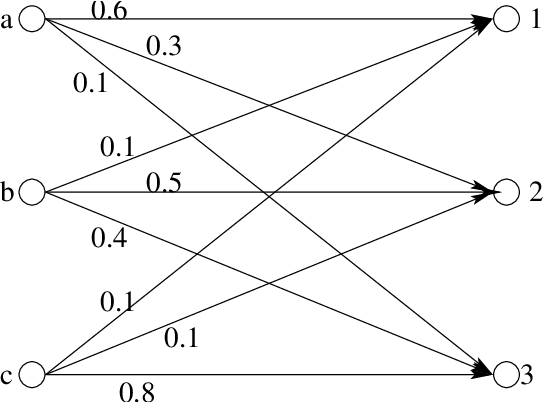
   The source sends a, b, and c with the following probabilities:

   
   1. Compute all (nine) conditional probabilities of the form P(X|Y ) for X ∈{a,b,c} and Y ∈{1, 2, 3}.
   2. Compute all (nine) joint probabilities of the form P(X,Y ) for X ∈{a,b,c} and Y ∈{1, 2, 3}.
   3. A receiver makes decisions as follows:
      • If 1 is received, decide a was sent.
      • If 2 is received, decide b was sent.
      • If 3 is received, decide c was sent.

      What is the probability that this receiver makes a wrong decision? (I.e.., its decision is different from what was actually sent.)

   4. What is the best receiver decision rule (assignment from 1, 2, 3 to a, b, c)?
   5. What is the resulting probability of error?
2. Consider a random variable X having a double-exponential (Laplacian) density,

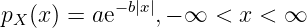
   where a and b are positive constants.

   1. Determine the relationship between a and b such that p_X(x) is a valid density function.
   2. Determine the corresponding probability distribution function P_X(x).
   3. Find the probability that the random variable lies between 2 and 3.
   4. What is the probability that X lies between 2 and 3 given that the magnitude of X is less than 3.
3. Let x₁, x₂, …, x_N be a set of N identically distributed statistically independent random variables, each with density function p_x and distribution function F_x. These variables are applied to a system that selects as its output, y_N, the largest of the {x_i}, i.e., y_N = max{x₁,x₂,…,x_N}. Clearly, y_N is a random variable.
   1. Express p_yN in terms of N, p_x, and F_x.
   2. Assume now that the x_i are exponentially distributed random variables:

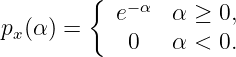
      Calculate the expectation E[y_N] for N = 1, 2.

4. Path Loss and SNR Friis transmission equation

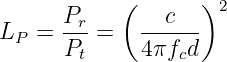
   describes the path loss L_p under line-of-sight propagation conditions as a signal travels from transmitter to receiver.

   1. Convert the path loss expression above to a logarithmic scale (i.e., to dB) by taking 10 log ₁₀(⋅) of both sides of the relationship.
   2. The transmitter of a communication system sends signals with the following parameters:
      • transmit power P_t = 10dBm
      • bandwidth W = 10MHz
      • carrier frequency f_c = 1GHz

      Compute the received power P_r, as a function of the distance d between transmitter and receiver. Express P_r in dBm, i.e., compute 10 log ₁₀().

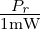   3. The communication system is impaired by thermal noise and is designed so that a signal-to-noise ratio 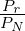of at least 10 dB is required for successful operation. What is the maximum distance d for which the system will work?