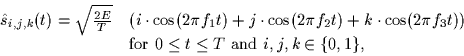Parity Check Code

In this problem, we analyze the use of a simple coding technique referred to as parity check coding for reducing the error rate in a communication system. Throughout this problem, equally likely messages are to be transmitted over an additive white Gaussian noise channel with spectral height 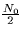$\frac{N_0}{2}$.

1.

Consider first the following quaternary signal set

$$s_{i,j}(t) = \sqrt{\frac{2E}{T}} \left( i \cdot \cos(2\pi f... ...ht) \mbox{for $0 \leq t \leq T$\space and $i,j\in\{0,1\}$}.$$

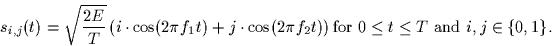
Hence, there are four signals. You may assume that f₁T and f₂T are distinct integers.
Draw and accurately label a signal space diagram showing the four signals and the decision boundaries formed by the optimum receiver.

2.

Compute the minimum probability of error achievable with this signal set.

3.

Now the signal set is changed to  

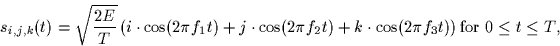$$s_{i,j,k}(t) = \sqrt{\frac{2E}{T}} \left( i \cdot \cos(2\pi... ...dot \cos(2\pi f_3 t) \right) \mbox{for $0 \leq t \leq T$},$$ (1)

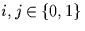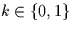where as before $i,j \in \{0,1\}$ and $k \in \{0,1\}$ is chosen such that i+j+k is an even number. Hence, the bit k can be thought of as a parity check bit.
Show that the signal set (1) can be thought of as a subset of the following signal set with eight signals  

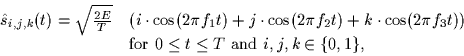$$\begin{array} {ll} \hat{s}_{i,j,k}(t) = \sqrt{\frac{2E}{T}}... ...$0 \leq t \leq T$\space and $i,j,k \in \{0,1\}$}, \end{array}$$ (2)

by representing the signal set (2) in an appropriately chosen signal space. Then, indicate which of the eight signals of set (2) are members of signal set (1).

4.

Now consider the minimum probability of error receiver for distinguishing between the signals of the set (2), i.e., the decision boundaries are planes orthogonal to the faces of a cube. If the observation falls into the decision region belonging to one of the four signals in set (1) the receiver decides in favor of that signal. Otherwise, the receiver declares that an error has been detected.
What is the probability that an error is detected?

5.

What is the probability that an error goes undetected?

6.

Bonus (10pts.): Is the decision rule in part (d) optimum for distinguishing between the signals in set (1)? If yes, explain why. If not, illustrate the optimum decision regions in signal space.