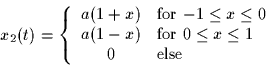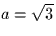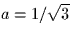Next: Amplitude Modulation and Sampling
Up: Collected Problems
Previous: Parity Check Code
(check all correct answers)
- 1.
- Consider a system in which the output y(t) is generated by
multiplying the input x(t) by
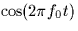 . Which of the
following is true?
. Which of the
following is true?
- The system is a linear system.
- The system is not linear.
- The system is time-invariant.
- The system is not time-invariant.
- 2.
- A system is given by the input-output relationship
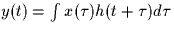 . Which of the following is true?
. Which of the following is true?
- The system is a linear system.
- The system is not linear.
- The system is time-invariant.
- The system is not time-invariant.
- 3.
- Let x1(t) be a rectangular pulse of width 1, i.e.,
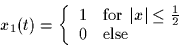
Further, let x2(t) be a triangular pulse,
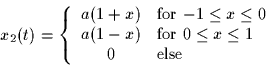
Which value of a makes the energy of the two signals equal?
- a=1
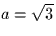
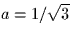
- none of the above.
- 4.
- Let the amplitude a of the triangular pulse be such that the
energies of both signals in the previous question are the same. Then,
each of the two signals is input to an ideal lowpass filter with
cut-off frequency 1; the resulting output signals are denoted
y1(t) and y2(t). Which of the following is true?
- The energy of y1(t) is larger than the energy of y2(t).
- The energy of y1(t) is smaller than the energy of y2(t).
- The energy of y1(t) is the same as the energy of y2(t).
- The question can not be answered with the information provided.



Next: Amplitude Modulation and Sampling
Up: Collected Problems
Previous: Parity Check Code
Prof. Bernd-Peter Paris
3/3/1998
![]()