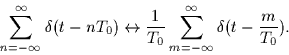Next: Real-valued Systems
Up: Collected Problems
Previous: Multiple-Choice Questions
Consider the system in the block diagram below.
The input signal x(t) is an amplitude modulated signal given by
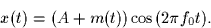
The constant A is large enough that A + m(t) is positive for all
t. Further, the message bearing signal m(t) is strictly
band-limited, i.e., M(f)=0 for |f|>fm and 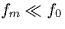 .
.
- 1.
- Compute the Fourier transform X(f) of the input signal x(t).
- 2.
- Show that the following is a Fourier transform pair
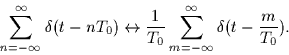
- 3.
- The input signal is sampled by the impulse train.
Are the conditions of the sampling theorem discussed in class
satisfied? Explain!
- 4.
- Assume that the sampling rate equals the carrier frequency,
i.e.,
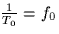 . Compute the Fourier transform Y(f) of
the signal y(t).
. Compute the Fourier transform Y(f) of
the signal y(t).
- 5.
- Compute the output z(t) under the assumptions that the lowpass
filter is ideal and it's cut-off
frequency fc satisfies
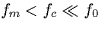 .
.
Prof. Bernd-Peter Paris
3/3/1998
![\begin{picture}
(60,30)
\setlength {\unitlength}{1mm}
\put( 0, 20){\vector(...
... 0)[t]
{$\displaystyle \sum_{n=-\infty}^{\infty} \delta(t-nT_0)$}}\end{picture}](img74.gif)
![\begin{picture}
(60,30)
\setlength {\unitlength}{1mm}
\put( 0, 20){\vector(...
... 0)[t]
{$\displaystyle \sum_{n=-\infty}^{\infty} \delta(t-nT_0)$}}\end{picture}](img74.gif)
![]()