


Up: Collected Problems
Previous: Amplitude Modulation and Sampling
Throughout this problem, h(t) is a real-valued function which denotes the
impulse response of a system.
- 1.
- Which condition must h(t) satisfy to be the impulse response
of a causal system?
- 2.
- Show that the Fourier transform of an even, real-valued signal
x(t) is purely real, i.e., X(f) = X*(f).
- 3.
- Show that the Fourier transform of an odd, real-valued signal y(t)
is purely imaginary, i.e., Y(f) = -Y*(f).
- 4.
- Confirm that an arbitrary real-valued impulse response h(t) can
always be decomposed into an even part he(t) and an odd part
ho(t), both real-valued:
h(t) = he(t) + ho(t),
with
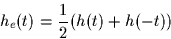
and
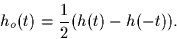
Note: You have to show that he(t) and ho(t) are even and odd,
respectively and that h(t) = he(t) + ho(t).
- 5.
- Combining the results in parts (b)-(d), formulate simple rules
for computing only the real part or only the imaginary part of the
Fourier transform of a real-valued impulse response.
- 6.
- Verify your rules by considering the example h(t)=1 for
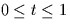 .
.
Prof. Bernd-Peter Paris
3/3/1998
![]()
![]()
![]()
![]()