


Next: Parity Check Code
Up: Collected Problems
Previous: AM Stereo Signals
The following signal set is used to transmit equally likely messages over an
additive white Gaussian noise channel (autocorrelation function 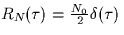 ):
):
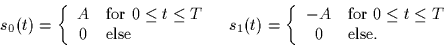
- 1.
- Draw and accurately label a block diagram of the receiver which minimizes
the probability of error and utilizes a single matched filter followed
by a sampler. Sketch the impulse response of the matched filter.
- 2.
- Compute the minimum probability of error achievable with this signal set.
- 3.
- For the remainder of the problem the following receiver is used:
Compute the impulse response of the RC-circuit at the front end of the
receiver above, i.e., what signal
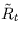 would you observe if the input
signal were
would you observe if the input
signal were 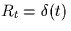 ?
?
- 4.
- Assume now that the impulse response of the RC-circuit is
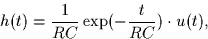
where u(t) denotes the unit
step function. Find the distribution of the
random variable
R, i.e., the sample taken from 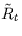 at t=T, for both cases:
s0(t) was transmitted or s1(t) was transmitted.
at t=T, for both cases:
s0(t) was transmitted or s1(t) was transmitted.
- 5.
- Compute the probability of error for the receiver above and compare it to
the probability of error for the optimum receiver.



Next: Parity Check Code
Up: Collected Problems
Previous: AM Stereo Signals
Prof. Bernd-Peter Paris
3/3/1998
![]()
![\begin{picture}
(870,190)(110,490)
\setlength {\unitlength}{0.0065in}
%
%%
\...
...){\vector( 1, 0){ 50}}
\put(930,593){\makebox(50,0)[b]{$\hat{b}$}}\end{picture}](img41.gif)
![]()