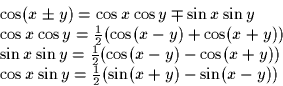Next: Binary Receivers
Up: Collected Problems
Previous: Suboptimum Receiver
The use of quadrature carrier multiplexing provides the basis for the
generation of AM stereo signals. One particular form of such a signal is
described by
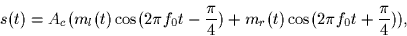
where fc is the carrier frequency and ml(t) and mr(t) are the left-hand and
right-hand output signals of the loudspeakers, respectively.
You may assume throughout that ml(t) and mr(t) are lowpass signals with bandwidth
fm much smaller than f0.
- 1.
- Draw a block diagram of a system with inputs ml(t) and mr(t) that
generates the signal s(t).
- 2.
- Compute the Fourier transform of the signal s(t).
- 3.
- A coherent mono receiver can be implemented as in the following block
diagram:
Derive an expression for the signal c(t) and then compute the Fourier
transform of the signal c(t).
- 4.
- Assume the lowpass filter to be ideal with cut-off frequency fc satisfying
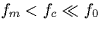 , find an expression for the output signal
, find an expression for the output signal 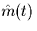 . Explain how the mono receiver processes the received signal containing stereo
signals.
. Explain how the mono receiver processes the received signal containing stereo
signals.
- 5.
- Now a stereo receiver as shown in the following block diagram is employed:
Proceeding as in parts (c) and (d), compute expressions for the two signals
c1(t) and c2(t).
Then determine how the coefficients ai, i=1,2,3,4 must be chosen such
that the original left-hand and right-hand signals ml(t) and mr(t) are
recovered.
Hint:
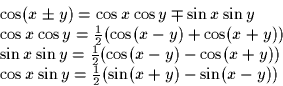



Next: Binary Receivers
Up: Collected Problems
Previous: Suboptimum Receiver
Prof. Bernd-Peter Paris
3/3/1998
![]()
![\begin{picture}
(300,120)(40,550)
\setlength {\unitlength}{0.008in}
%
\thic...
...ector( 1, 0){ 60}}
\put(280,625){\makebox(60, 0)[b]{$\hat{m}(t)$}}\end{picture}](img34.gif)
![\begin{picture}
(620,300)(80,450)
\setlength {\unitlength}{0.008in}
%
\thic...
...0){\vector( 1, 0){ 60}}
\put(640,525){\makebox(60,0)[b]{$m_l(t)$}}\end{picture}](img37.gif)