Homework 2 (Due: September 18)

[PDF]

Reading:

Goldsmith chapters 2 and 3.

Problems

1. Link Budget
   A wireless communication system’s transmitted signals are attenuated according to the following path loss model: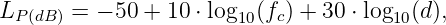

   where d denotes the distance between transmitter and receiver in meters and the carrier frequency f_c = 1 GHz. Further, the system is characterized by

   • transmit and receive antenna gains G_T = G_R = 0 dB,
   • receiver implementation loss L_R = 2 dB,
   • noise figure F = 2 dB,
   • thermal noise PSD kT₀ = -174 dBm/Hz,
   • signal bandwidth and symbol rate B = R_S = 1 MHz,
   • required 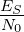= 10 dB.
   1. Compute the receiver sensitivity.
   2. Assuming the transmitter power equals 1 Watt, what is the transmission range d?
   3. How much transmit power is required to communicate over a distance of 2 km.
   4. For a given transmit power, by how much does the range increase if the symbol rate R_S is reduced to 100 KHz?
   5. Assume now that the path loss is subject to log-normal fading with standard deviation σ = 4 dB. Assume further that the system is characterized by the parameters tabulated above and that the transmit power equals P_t = 30 dBm.

      What is the probabability that 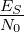is below 10 dB?

   6. What provisions must be made to ensure that the probability that 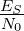is below 10 dB is smaller than 10^-3?
2. Modify the MATLAB function two_ray_loss.m to include a second reflector. For example, you may include a wall behind one of the antennas. Plot the resulting path loss; you may use plot_two_ray_loss.m as a starting point. Describe what you did and explain if the path loss makes sense.
3. Goldsmith: Problem 2.18
4. Goldsmith: Problem 2.23
5. Goldsmith: Problem 2.25