- Frequency-Shift Keying (FSK)
In a coherent FSK signalling scheme the signals s1(t) and s2(t) are defined to be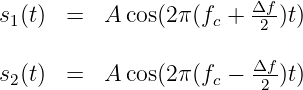
These signals are used to transmit equally-likely bits over a channel which adds white Gaussian noise of spectral height
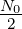 to the
signal.
to the
signal.
- Assuming fc ≫ Δf, show that the “correlation coefficient” ρ
of the signals s1(t) and s2(t), defined as
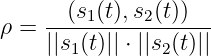
is given approximately by
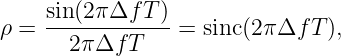
where T is the duration of a bit interval.
- What is the minimum value of the frequency shift Δf for which the signals are orthogonal?
- Draw a block diagram of the receiver which attains the minimum probability of error.
- Compute the minimum probability of error as a function of ρ.
- What is the value of Δf that minimizes the probability of error?
- Assuming fc ≫ Δf, show that the “correlation coefficient” ρ
of the signals s1(t) and s2(t), defined as
- Binary Signal Sets
Information bits are to be transmitted over an additive, white Gaussian noise channel (spectral height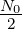 ) using the depicted signal
set.
) using the depicted signal
set.
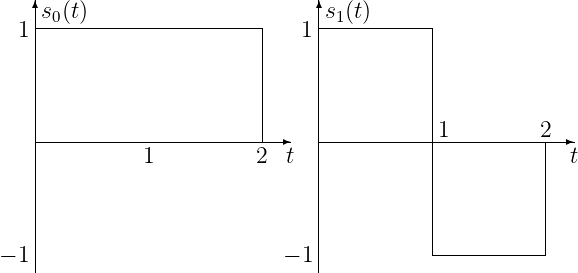
- Draw the block diagram of the minimum probability of error receiver.
- Compute the probability of error attained by this receiver.
- Repeat parts (a) and (b) for the following signal set:
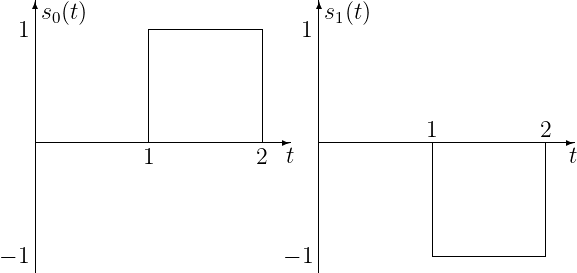
- Compare the results for the two signal sets and explain.
- Suboptimum Receivers
The Cheap and Dirty Communications Company has designed yet another digital communication system. The binary signal set consists of sinusoids having duration T and frequencies f0 = n∕T and f1 = m∕T, respectively (n and m distinct integers). These signals are equally likely. The channel adds white Gaussian noise of spectral height N0∕2. An average bit error rate of at most 10-3 is required. The transmitter is amplitude-limited: sinusoids can not have higher amplitude than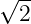 A0.
A0.
- What is the minimum probability of error receiver?
- What is the maximum data rate (bits/second) that can be transmitted through the channel?
- The designer can save some expense (true to the name of the company) by simplifying the receiver. Instead of using sinusoids in the correlator of the receiver, square waves of the same frequency and phase are used to reduce hardware costs. Analyze the effect of this less expensive receiver on the performance of the communication system.
- To save even more, the designer decides to remove the synchronization circuit, such that the phase difference between the received signal and the local square-wave oscillators can assume any value between 0 and 2π with equal probability. What changes in the receiver are required to maintain reasonable performance?
- What is the probability of error attained by your receiver from part (d)?
- Consider the signal
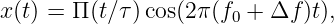
where Π(x) = 1 if |x| <
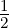 and Π(x) = 0 if |x| >
and Π(x) = 0 if |x| > 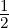 . You may assume
that Δf ≪ f0. Let x(t) be the input to a filter with impulse
response
. You may assume
that Δf ≪ f0. Let x(t) be the input to a filter with impulse
response
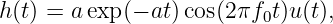
where u(t) denotes the unit step function. Find the output using baseband-equivalent signal techniques.