


Next: Homework 6
Up: Homework Assignments
Previous: Homework 4
ECE 630: Statistical Communication Theory
Prof. B.-P. Paris
Homework 5
Due March 4, 2003
- Reading
- Wozencraft & Jacobs: Chapter 4 and Chapter 8 pages 598-603.
- Problems
-
- Let
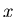 and
and 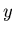 be elements of a normed linear vector space.
be elements of a normed linear vector space.
- Determine whether the following are valid inner products for the indicated
space.
-
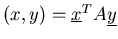 , where
, where 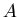 is a
nonsingular,
is a
nonsingular,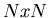 matrix and
matrix and 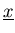 ,
, 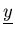 are elements of
the space of
are elements of
the space of 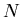 -dimensional vectors.
-dimensional vectors.
-
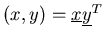 , where
, where 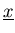 and
and
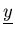 are elements of the space of
are elements of the space of 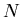 -dimensional (column!)
vectors.
-dimensional (column!)
vectors.
-
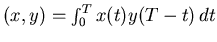 , where
, where 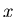 and
and 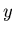 are finite energy
signals defined over
are finite energy
signals defined over ![$[0,T]$](img95.png) .
.
-
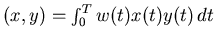 , where
, where 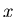 and
and 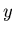 are finite energy
signals defined over
are finite energy
signals defined over ![$[0,T]$](img95.png) and
and 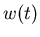 is a non-negative function.
is a non-negative function.
![$E[XY]$](img98.png) , where
, where  and
and 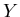 are real-valued random variables having finite
mean-square values.
are real-valued random variables having finite
mean-square values.
-
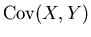 , the covariance of the real-valued random variables
, the covariance of the real-valued random variables  and
and 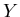 . Assume that
. Assume that  and
and 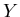 have finite mean-square values.
have finite mean-square values.
- Under what conditions is
a valid inner product for the space of finite-energy functions defined over
![$[0,T]$](img95.png) ?
?
- Consider the vectors
- Use the Gram-Schmidt procedure to find orthonormal basis vectors
which span the space of these vectors.
- What is the dimension of the space spanned by these three
vectors?
- Compute the representation of the
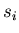 in terms of the
orthonormal basis vectors determined in part (a).
in terms of the
orthonormal basis vectors determined in part (a).
- Repeat parts (a)-(c) for the signals
- The following signals are used to communicate one of two
equally likely messages over a channel perturbed by a zero mean, white
Gaussian random process,
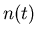 , with spectral height
, with spectral height 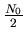 ,
,
- Use the Gram-Schmidt procedure to find orthonormal functions
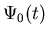 and
and 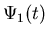 to represent
to represent 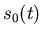 and
and 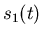 .
.
- Sketch the signals
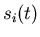 and the basis functions
and the basis functions 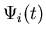 .
.
- Express
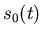 and
and 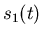 in terms of the basis functions
in terms of the basis functions
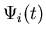 .
.
- Define the random variables
Find the joint density function of 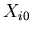 and
and 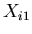 .
.
- Define the random variables
Find the joint density function of 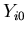 and
and 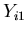 .
.



Next: Homework 6
Up: Homework Assignments
Previous: Homework 4
Dr. Bernd-Peter Paris
2003-05-01
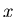 and
and 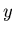 be elements of a normed linear vector space.
be elements of a normed linear vector space.
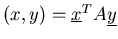 , where
, where 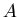 is a
nonsingular,
is a
nonsingular,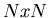 matrix and
matrix and 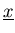 ,
, 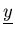 are elements of
the space of
are elements of
the space of 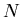 -dimensional vectors.
-dimensional vectors.
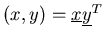 , where
, where 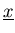 and
and
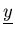 are elements of the space of
are elements of the space of 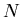 -dimensional (column!)
vectors.
-dimensional (column!)
vectors.
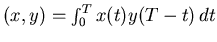 , where
, where 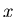 and
and 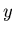 are finite energy
signals defined over
are finite energy
signals defined over ![$[0,T]$](img95.png) .
.
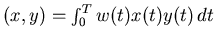 , where
, where 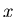 and
and 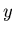 are finite energy
signals defined over
are finite energy
signals defined over ![$[0,T]$](img95.png) and
and 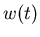 is a non-negative function.
is a non-negative function.
![$E[XY]$](img98.png) , where
, where  and
and 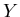 are real-valued random variables having finite
mean-square values.
are real-valued random variables having finite
mean-square values.
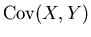 , the covariance of the real-valued random variables
, the covariance of the real-valued random variables  and
and 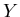 . Assume that
. Assume that  and
and 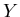 have finite mean-square values.
have finite mean-square values.
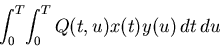
![$[0,T]$](img95.png) ?
?
![\begin{displaymath}
\begin{array}{ccc}
s_0 = \left[ \begin{array}{c} 1 1 1...
... \begin{array}{c} 1 4 9 \end{array} \right].
\end{array}\end{displaymath}](img101.png)
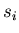 in terms of the
orthonormal basis vectors determined in part (a).
in terms of the
orthonormal basis vectors determined in part (a).
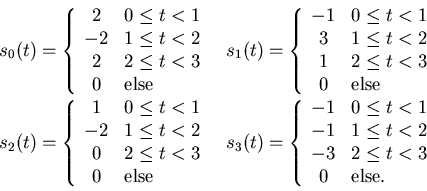
 , with spectral height
, with spectral height  ,
,
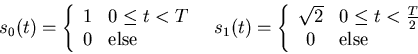
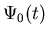 and
and 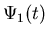 to represent
to represent 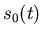 and
and 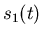 .
.
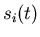 and the basis functions
and the basis functions 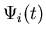 .
.
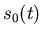 and
and 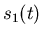 in terms of the basis functions
in terms of the basis functions
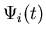 .
.
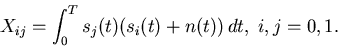
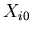 and
and 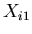 .
.
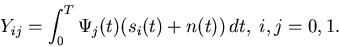
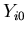 and
and 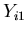 .
.