- The stationary random process
 is passed through a linear filter with
transfer function
is passed through a linear filter with
transfer function 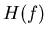 ,
,

The output process is labeled . The mean of
. The mean of  is measured to be
is measured to be
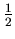 and the covariance function of
and the covariance function of  is found to be
is found to be
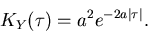
- Compute the power spectral density of
 .
.
- Find the second order description of
 .
.
- Compute the power spectral density of
- In practice one often wants to measure the power spectral density of a
stochastic
process. For the purposes of this problem, assume the process
 is
wide-sense stationary, zero mean, and Gaussian. The following measurement
system is proposed.
is
wide-sense stationary, zero mean, and Gaussian. The following measurement
system is proposed.

Here
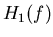 is the transfer function of an ideal bandpass filter and
is the transfer function of an ideal bandpass filter and 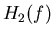 is an ideal lowpass,
is an ideal lowpass,

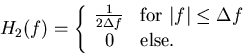
Assume that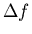 is small compared to the range of frequencies over which
is small compared to the range of frequencies over which
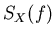 varies, i.e., you may assume that
varies, i.e., you may assume that 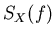 is constant over intervals
of width
is constant over intervals
of width 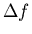 .
.
- Find the mean and correlation function of
 in terms of the second
order description of
in terms of the second
order description of  .
.
- Compute the the power spectral density of the process
 .
.
- Compute the expected value of
 .
.
- By considering the variance of
 , comment on the accuracy of this
measurement of the power density of the process
, comment on the accuracy of this
measurement of the power density of the process  .
.
- Find the mean and correlation function of
- The price of a certain stock can fluctuate during the day while the
``true'' value is rising or falling. To facilitate financial decisions, a Wall
street broker decides to use stochastic process theory. The price
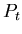 of a
stock is described by
of a
stock is described by

where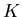 is the constant our knowledgeable broker is seeking and
is the constant our knowledgeable broker is seeking and 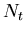 is a
stochastic process describing the random fluctuations.
is a
stochastic process describing the random fluctuations. 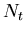 is a white,
Gaussian process having spectral height
is a white,
Gaussian process having spectral height 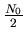 . The broker decides to
estimate
. The broker decides to
estimate 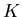 according to:
according to:
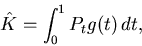
where the ``best'' function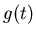 is to be found.
is to be found.
- Find the probability density function of the estimate
 for any
for any
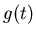 the broker might choose.
the broker might choose.
- A simple-minded estimate of
 is to use simple averaging (i.e.,
set
is to use simple averaging (i.e.,
set 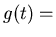 constant). Find the value of the constant which results in
constant). Find the value of the constant which results in
![$E[\hat{K}] =
K$](img82.png) . What is the resulting percentage error as expressed by
. What is the resulting percentage error as expressed by
![$\sqrt{var[\hat{K}]}/\vert E[\hat{K}]\vert$](img83.png) ?
?
- Use
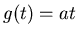 and choose
and choose  to yield
to yield
![$E[\hat{K}] =
K$](img82.png) . How much better is this choice than simple averaging?
. How much better is this choice than simple averaging?
- DO you think
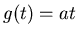 is the best possible choice? Why or why not?
is the best possible choice? Why or why not?
- Find the probability density function of the estimate