


Next: Homework 4
Up: Homework Assignments
Previous: Homework 2
ECE 630: Statistical Communication Theory
Prof. B.-P. Paris
Homework
3
Due Feb. 11, 2003
- Reading
- Wozencraft & Jacobs: Chapter 3, pages 129-199.
- Problems
-
- Wozencraft & Jacobs: Problem 3.10
- Let
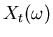 be a stochastic process defined on
be a stochastic process defined on
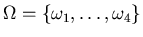 having probabibility assignments
having probabibility assignments
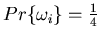 for
for 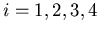 . The sample functions are
. The sample functions are
- Compute the joint probability
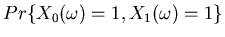 .
.
- Compute the conditional probability
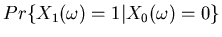 .
.
- Compute the mean and correlation function of
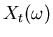 .
.
- Is this process stationary? wide-sense stationary?
- A stochastic process is defined by
where the frequency 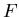 is uniformly distributed over the interval
is uniformly distributed over the interval ![$[0,f_0]$](img50.png) .
.
- Find the mean and correlation function of
 .
.
- Show that this process is non-stationary.
Now suppose we redefine the process  to be
to be
where 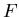 and
and 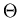 are statistically independent random variables.
are statistically independent random variables. 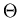 is uniformly disributed over
is uniformly disributed over ![$[-\pi,\pi]$](img54.png) and
and 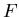 is distributed as before.
is distributed as before.
- Compute the mean and correlation function of
 .
.
- Is
 wide-sense stationary? Show your reasoning.
wide-sense stationary? Show your reasoning.
- Find the first order density
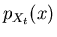 .
.
- Let
 be a wide-sense stationary stochastic process. Let
be a wide-sense stationary stochastic process. Let 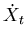 denote the derivative of
denote the derivative of  .
.
- Compute the expected value and correlation function of
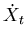 in
terms of the expected value and correlation function of
in
terms of the expected value and correlation function of  .
.
- Under what conditions are
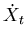 and
and  orthogonal, i.e.,
orthogonal, i.e.,
![$\mbox{\bf E}[\dot{X}_t X_t] = 0$](img57.png) ?
?
- Compute the mean and correlation function of
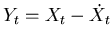 .
.
- The bandwidth of the process
 can be defined by
can be defined by
Express this definition in terms of the mean and correlation functions of  and
and 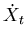 .
.



Next: Homework 4
Up: Homework Assignments
Previous: Homework 2
Dr. Bernd-Peter Paris
2003-05-01
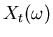 be a stochastic process defined on
be a stochastic process defined on
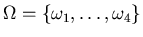 having probabibility assignments
having probabibility assignments
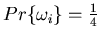 for
for 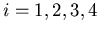 . The sample functions are
. The sample functions are
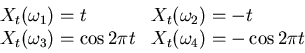
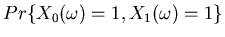 .
.
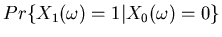 .
.
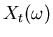 .
.
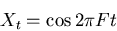
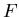 is uniformly distributed over the interval
is uniformly distributed over the interval ![$[0,f_0]$](img50.png) .
.
 .
.
 to be
to be
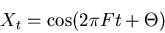
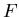 and
and 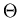 are statistically independent random variables.
are statistically independent random variables. 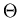 is uniformly disributed over
is uniformly disributed over ![$[-\pi,\pi]$](img54.png) and
and 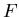 is distributed as before.
is distributed as before.
 .
.
 wide-sense stationary? Show your reasoning.
wide-sense stationary? Show your reasoning.
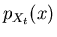 .
.
 be a wide-sense stationary stochastic process. Let
be a wide-sense stationary stochastic process. Let 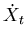 denote the derivative of
denote the derivative of  .
.
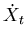 in
terms of the expected value and correlation function of
in
terms of the expected value and correlation function of  .
.
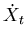 and
and  orthogonal, i.e.,
orthogonal, i.e.,
![$\mbox{\bf E}[\dot{X}_t X_t] = 0$](img57.png) ?
?
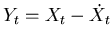 .
.
 can be defined by
can be defined by
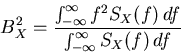
 and
and 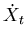 .
.