


Next: Homework 3
Up: Homework Assignments
Previous: Homework 1
ECE 630: Statistical Communication Theory
Prof. B.-P. Paris
Homework
2
Due Feb. 4, 2003
- Reading
- Wozencraft & Jacobs: Chapter 2 pages 58-114.
- Problems
-
- Wozencraft & Jacobs: Problem 2.30
- Let
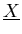 be a zero mean Gaussian random vector with covariance
matrix
be a zero mean Gaussian random vector with covariance
matrix 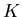 .
.
- Give an expression for the density function
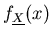 .
.
- If
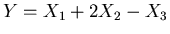 , find
, find 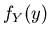 .
.
- If the vector
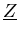 has components defined by
has components defined by
determine
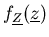 . What are the properties of the new
random vector?
. What are the properties of the new
random vector?
- Determine
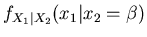
- Characteristic Function of Gaussian Random Variables
- Show that the characteristic function of a Gaussian random variable
 having mean
having mean 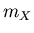 and variance
and variance 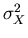 is
is
- Find the characteristic function of a Gaussian random vector having mean
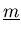 and covariance matrix
and covariance matrix 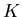 .
.
- Use this result to show that the components of a Gaussian random vector
are Gaussian.
- Show that the n-th central moment of a Gaussian random variable is given
by
- We are concerned about the values of the two random variables
 and
and 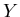 .
However, we can only observe the values of
.
However, we can only observe the values of 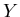 . We wish to estimate
(i.e. guess intelligently) the value of
. We wish to estimate
(i.e. guess intelligently) the value of  by using a wisely chosen function
by using a wisely chosen function
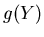 of the observed value
of the observed value 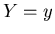 . Let
. Let 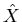 denote this estimate,
denote this estimate,
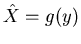 .
.
- Show that the mean-square estimation error
is minimized by choosing
![$g(y)=\mbox{\bf E}[X \vert Y=y]$](img33.png) , where
, where
![$\mbox{\bf E}[X \vert
Y=y]$](img34.png) denotes the conditional expected value of
denotes the conditional expected value of  given the observation of
given the observation of
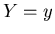 ,
,
- Let
 and
and 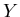 be jointly distributed, zero mean Gaussian random
variables with variances
be jointly distributed, zero mean Gaussian random
variables with variances 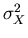 and
and 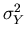 and correlation
coefficient
and correlation
coefficient 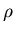 . Show that the conditional expected value of
. Show that the conditional expected value of  given
given
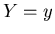 is a Gaussian random variable with mean
is a Gaussian random variable with mean
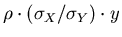 and variance
and variance
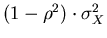 .
.
- We wish to estimate
 based on the observation of
based on the observation of 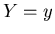 ; however we wish
to restrict the estimate to be linear:
; however we wish
to restrict the estimate to be linear:
Find the values of 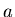 and
and 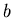 that minimize the mean-square estimation error.
that minimize the mean-square estimation error.
- Of the estimators defined in part (a) and part (c) of this problem, which
do you think will be ``better'' in general? Which do you think will be easier
to compute? Give reasons for your answers.



Next: Homework 3
Up: Homework Assignments
Previous: Homework 1
Dr. Bernd-Peter Paris
2003-05-01
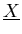 be a zero mean Gaussian random vector with covariance
matrix
be a zero mean Gaussian random vector with covariance
matrix 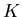 .
.
![\begin{displaymath}
K = \left[ \begin{array}{ccc} 3 & 3 & 0 3 & 5 & 0 0 & 0 & 6
\end{array} \right]
\end{displaymath}](img14.png)
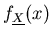 .
.
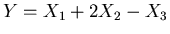 , find
, find 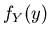 .
.
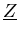 has components defined by
has components defined by
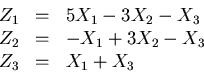
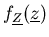 . What are the properties of the new
random vector?
. What are the properties of the new
random vector?
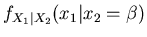
 having mean
having mean 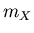 and variance
and variance 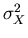 is
is
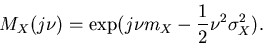
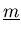 and covariance matrix
and covariance matrix 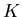 .
.
![\begin{displaymath}
\mbox{\bf E}[(X-m_X)^n] = \left\{
\begin{array}{cl}
1 \cdo...
...X^n & \mbox{n even} \\
0 & \mbox{n odd}
\end{array} \right.
\end{displaymath}](img26.png)
 and
and 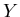 .
However, we can only observe the values of
.
However, we can only observe the values of 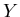 . We wish to estimate
(i.e. guess intelligently) the value of
. We wish to estimate
(i.e. guess intelligently) the value of  by using a wisely chosen function
by using a wisely chosen function
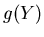 of the observed value
of the observed value 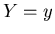 . Let
. Let 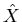 denote this estimate,
denote this estimate,
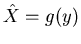 .
.
![\begin{displaymath}
\epsilon = \mbox{\bf E}[(X-\hat{X})^2]
\end{displaymath}](img32.png)
![$g(y)=\mbox{\bf E}[X \vert Y=y]$](img33.png) , where
, where
![$\mbox{\bf E}[X \vert
Y=y]$](img34.png) denotes the conditional expected value of
denotes the conditional expected value of  given the observation of
given the observation of
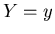 ,
,
![\begin{displaymath}
\mbox{\bf E}[X \vert Y=y] = \int_{-\infty}^{\infty} x f_{X\vert Y}(x\vert Y=y) dx.
\end{displaymath}](img35.png)
 and
and 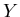 be jointly distributed, zero mean Gaussian random
variables with variances
be jointly distributed, zero mean Gaussian random
variables with variances 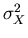 and
and 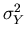 and correlation
coefficient
and correlation
coefficient 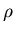 . Show that the conditional expected value of
. Show that the conditional expected value of  given
given
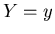 is a Gaussian random variable with mean
is a Gaussian random variable with mean
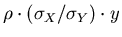 and variance
and variance
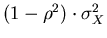 .
.
 based on the observation of
based on the observation of 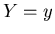 ; however we wish
to restrict the estimate to be linear:
; however we wish
to restrict the estimate to be linear:
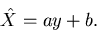
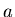 and
and 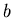 that minimize the mean-square estimation error.
that minimize the mean-square estimation error.