


Next: Homework 2
Up: Homework Assignments
Previous: Homework Assignments
ECE 630: Statistical Communication Theory
Prof. B.-P. Paris
Homework 1
Due Jan. 27, 2003
- Reading
- Wozencraft & Jacobs: Chapter 1 and Chapter 2 up to page 58.
- Problems
-
- Wozencraft & Jacobs: Problem 2.7
- Wozencraft & Jacobs: Problem 2.11
- Consider a random variable
 having a double-exponential (Laplacian)
density,
having a double-exponential (Laplacian)
density,
where 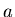 and
and 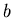 are positive constants.
are positive constants.
- Determine the relationship between
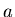 and
and 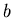 such that
such that 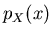 is a valid density function.
is a valid density function.
- Determine the corresponding probability distribution function
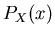 .
.
- Find the probability that the random variable lies between 1 and 2.
- What is the probability that
 lies between 1 and 2 given
that the magnitude of
lies between 1 and 2 given
that the magnitude of  is less than 2.
is less than 2.
- Melvin Fooch, a former student in ECE 630, has found
that the hours he spends working (
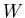 ) and sleeping (
) and sleeping (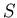 )
in preparation for the quiz are random variables having the joint density
)
in preparation for the quiz are random variables having the joint density
What Melvin does not know, and even his best friends will not tell him,
is that working only furthers his confusion and that his grade 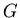 is
given by
is
given by
- Determine the constant
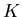 .
.
- What is the probability that the maximum time he devotes to
either working or sleeping is less than 10 hours?
- The instructor will pass poor Melvin if he achieves a grade of
75 or greater. What is the probability that this will occur?



Next: Homework 2
Up: Homework Assignments
Previous: Homework Assignments
Dr. Bernd-Peter Paris
2003-05-01
 having a double-exponential (Laplacian)
density,
having a double-exponential (Laplacian)
density,
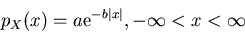
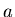 and
and 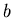 are positive constants.
are positive constants.
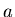 and
and 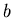 such that
such that 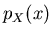 is a valid density function.
is a valid density function.
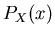 .
.
 lies between 1 and 2 given
that the magnitude of
lies between 1 and 2 given
that the magnitude of  is less than 2.
is less than 2.
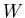 ) and sleeping (
) and sleeping (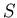 )
in preparation for the quiz are random variables having the joint density
)
in preparation for the quiz are random variables having the joint density
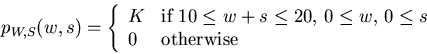
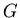 is
given by
is
given by
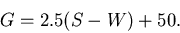
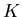 .
.