Next: Homework 7
Up: Homework Assignments
Previous: Homework 5
ECE 630: Statistical Communication Theory
Prof. B.-P. Paris
Homework 6
Due March 25, 2003
- Reading
- Wozencraft & Jacobs: Chapter 4. Another reference for
this material is: H.L. van Trees, "Detection Estimation, and
Modulation Theory," pp. 239-257.
- Problems
-
- Let the covariance function of a wide sense stationary process
be
Find the eigenfunctions and eigenvalues associated with the
Karhunen-Loeve expansion of  over
over 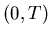 with
with 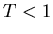 .
.
- Wozencraft & Jacobs: Problem 4.1
- Wozencraft & Jacobs: Problem 4.2
- Wozencraft & Jacobs: Problem 4.5
- Binary Hypothesis Testing
The two hypotheses are of the form:
- Find the likelihood ratio.
- Compute the decision regions for various values of the threshold
in the likelihood ratio test.
Dr. Bernd-Peter Paris
2003-05-01
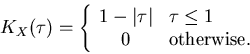
 over
over 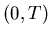 with
with 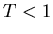 .
.