Homework 6 (Due: March 12)

[next] [prev] [prev-tail] [tail] [up]

Homework 6 (Due: March 12)

[PDF]

ECE 630: Statistical Communication Theory
Prof. B.-P. Paris
Homework 6
Due: March 12, 2019

Reading

Madhow: Section 3.2 and 3.3.

Problems

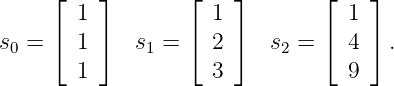
Consider the vectors $⌊ 1 ⌋ ⌊ 1 ⌋ ⌊ 1 ⌋ ⌈ ⌉ ⌈ ⌉ ⌈ ⌉ s0 = 1 s1 = 2 s2 = 4 . 1 3 9$
1. Use the Gram-Schmidt procedure to find orthonormal basis vectors which span the space of these vectors.
2. What is the dimension of the space spanned by these three vectors?
3. Compute the representation of the s_i in terms of the orthonormal basis vectors determined in part (a).
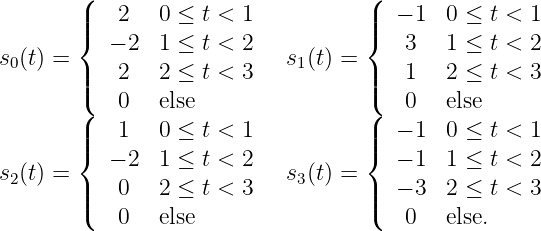
4. Repeat parts (a) — (c) for the signals $( ( ||{ 2 0 ≤ t < 1 ||{ - 1 0 ≤ t < 1 - 2 1 ≤ t < 2 3 1 ≤ t < 2 s0(t) = | 2 2 ≤ t < 3 s1(t) = | 1 2 ≤ t < 3 |( 0 else |( 0 else ( ( ||{ 1 0 ≤ t < 1 ||{ - 1 0 ≤ t < 1 s (t) = - 2 1 ≤ t < 2 s (t) = - 1 1 ≤ t < 2 2 || 0 2 ≤ t < 3 3 || - 3 2 ≤ t < 3 ( 0 else ( 0 else.$
Consider the Hilbert space L₂(-1, 1) of square integrable signals on the intervals [-1, 1]. The signals {1,t,t²} form a basis for a subspace of L₂(-1, 1).
- Apply the Gram-Schmidt procedure to the signals {1,t,t²} to generate an orthonormal basis {e_n}_n=0² of .
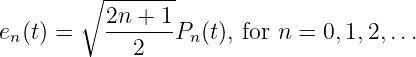
- It turns out that in general $∘ ------- e (t) = 2n-+-1P (t), for n = 0,1,2,... n 2 n$
  where P_n(t) are the Legendre polynomials
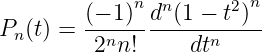
  $n n 2 n Pn (t) = (--1)- d-(1 --t)-- 2nn! dtn$
  Verify that the orthonormal basis signals that you computed via the Gram-Schmidt procedure equal those computed via the Legendre polynomials.
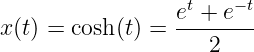
- Compute the projection of the signal $et + e-t x (t) = cosh (t) = -------- 2$
  onto the subspace . Express your answer as a second order polynomial.
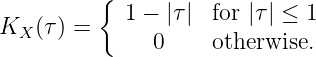
Karhunen-Loeve Expansion Let the covariance function of a wide-sense stationary process be ${ KX (τ) = 1 - |τ | for |τ| ≤ 1 0 otherwise.$
Find the eigenfunctions and eigenvalues associated with the Karhunen-Loeve expansion of X_t over (0,T) with T < 1.

[next] [prev] [prev-tail] [front] [up]