Homework 3 (Due: February 11)

[PDF]

Reading

review class notes.

Problems

1. Sinusoidal signals are very common and important for many communications systems. A sinusoidal signal is of the form²

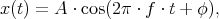
   where

   • A is called the amplitude of the signal; A is positive and indicates the largest value of the signal.
   • f i called the frequency of the sinusoid; f is positive and indicates how many times per second the sinusoid oscillates.
   • φ is called the phase; φ is between 0 and 2π and causes the sinusoid to move left and right.

   For this problem, you are to investigate how the power of a sinusoid varies with the parameters above. You are to construct a spread sheet similar to the one used in class to construct sinusoidal signals and measure their power. Note that this problem does not involve quantization. Throughout this problem, compute 100 samples at a rate of f_s = 200 samples per second.

   1. Set A = 1 and φ = 0 and measure the power of the sinusoid for the frequencies f = 10, 20, 25, 40, 50 Hz. Plot your results in a graph with f on the x-axis and power on the y-axis. Conclude how power depends on frequency. Does your conclusion make sense? Explain.
   2. Set f = 40 and φ = 0 and measure the power of the sinusoid for the amplitudes A = 0.5, 1, 2, 5, 10. Plot your results in a graph with A on the x-axis and power on the y-axis. Conclude how power depends on amplitude. Does your conclusion make sense? Explain.
   3. Set f = 40 and A = 1 and measure the power of the sinusoid for the phases φ = 0,π∕4,π∕2, 3π∕4. Plot your results in a graph with φ on the x-axis and power on the y-axis. Conclude how power depends on phase. Does your conclusion make sense? Explain.
2. Retrieve the spread sheet Quantization.xlsx from the course web site (it’s inside the “Transparencies” folder) and investigate how the SNR varies with the range V _max of an AD converter.
   1. Set the resolution N to 8 bits and leave the sampling rate at f_s = 1000 samples per second. Measure the SNR for the ranges V _max = 0.5, 1, 2, 5, 10, 20, 50, 100.
   2. Plot your results with V _max on the x-axis and SNR on the y-axis.
   3. Your graph should have the highest SNR for V _max = 5. Explain why SNR decreases for V _max < 5.
   4. Explain why SNR decreases for V _max > 5.
3. Convert from linear scale to dB and vice versa.
   1. Convert the following values to dB (try to do these without a calculator)
      1. 1
      2. 5
      3. 200
      4. 40,000,000
      5. 0.000,08
   2. Convert the following from dB to linear scale (try it without a calculator)
      1. 30dB
      2. 36dB
      3. -13dB
      4. -26dB
      5. -67dB
4. Express each of the following in signed magnitude, one’s complement, and two’s complement representation using 8 bits. Give your answers in binary and hexadecimal form:
   1. -45
   2. -126
   3. -1
   4. -127