[next] [prev] [prev-tail] [tail] [up]

Homework 2 (Due: February 4)

[PDF]

TCOM 500: Modern Telecommunications
Prof. B.-P. Paris
Homework 2
Due: February 4, 2010

Reading
Forouzan: Section 4.2 in Chapter 4.2 and Appendix B, review class notes.
Problems
  1. The signal1
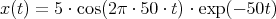
    x(t) = 5 ⋅ cos(2π ⋅ 50 ⋅ t) ⋅ exp(- 50t)

    is to be sampled at the rate of fs = 100 samples per second and then quantized assuming an input range of A∕Users∕pparis∕Home∕Courses∕tcom500∕in5 (i.e., between +5 and -5) and a resolution of N = 8 bits.

    • Compute the first five samples, i.e., the samples for t = 0, 0.01, 0.02, 0.03, 0.04.
    • Quantize the samples as indicated above.
    • For each sample compute the quantization error, i.e., the difference between the quantized and unquantized samples, and find the largest (absolute) error.
    • What is the largest possible quantization error that you could ever encounter with the above parameters?
    • Convert each of the quantized values to a binary representation consisting of the sign bit followed by N - 1 magnitude bits.
  2. Research commercially available AD converters (e.g., those offered by Analog Devices). Specifically, find an answer to the following questions:
    • What is the fastest (in terms of sampling rate) AD Converter that you can find.
    • What is the highest resolution (in terms of number of output bits) ADC that you can find.
    • For audio applications, ADCs with sampling rates of approximately 100K samples per second are needed. At that sampling rate, how does the price of such devices vary with resolution. Summarize your findings in a suitable graph.
    • For modern, wide-band radio applications sampling rates of 10MHz or more are needed. How does the price of such ADCs vary with resolution
  3. Perform a similar study for DA converters.

[next] [prev] [prev-tail] [front] [up]