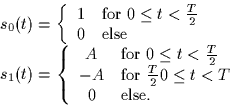
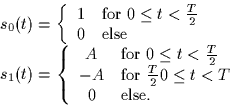
![\begin{picture}
(440,260)(40,530)
\setlength {\unitlength}{0.01in}
%
\put(14...
...0,0)[b]{$\phi_0(t)$}}
\put(140,540){\makebox(0,0)[b]{$\phi_1(t)$}}\end{picture}](img14.gif)
In the diagram above, the two functions ![]() and
and ![]() are chosen as:
are chosen as:
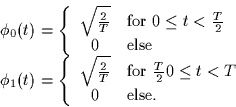
Compute the conditional distributions of the two integrator outputs. Notice that you will have to compute four such distributions: fR0|b=0, fR0|b=1, fR1|b=0 and fR1|b=1.
If your answer is yes, compute the values of a and b that minimize the probability of error and explain why optimum performance is achieved.
If your answer is no, compute the probability of error of the receiver in part (c) as a function of the coefficients a and b.