Timing Error

The following binary signal set is used to transmit equally likely messages over an additive white Gaussian noise channel (spectral height $\frac{N_0}{2}$),

$$\begin{array} {cl} s_0(t) = & \left\{ \begin{array} {cl} ... ...q t \leq T$}\\ 0 & \mbox{else} \end{array} \right.\end{array}$$

1.

Draw a block diagram of the optimum receiver which uses only a single correlator.

2.

Compute the probability of error for this receiver.

3.

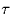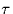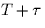Assume now that a receiver is used whose bit timing is off by $\tau$ seconds, such that the integration period is from $\tau$ to $T+\tau$. You may assume 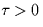$\tau \gt$. The resulting receiver is shown below.

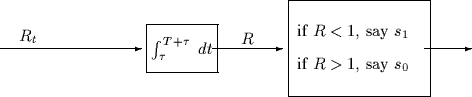
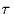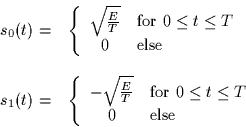
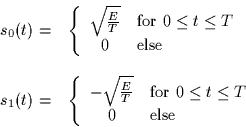
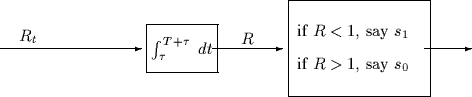
Compute the conditional probabilities, f_R|b=0 and f_R|b=1 as a function of the timing error $\tau$.

4.

Compute the probability of error as a function of the timing error $\tau$. How does the timing error affect performance relative to the optimum receiver?