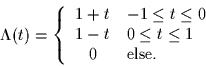Next: Binary Signals in AWGN
Up: Collected Problems
Previous: Collected Problems
Let the response of a linear time-invariant (LTI) system to 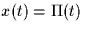 be
be
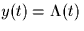 . Here
. Here 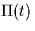 denotes the rectangular pulse:
denotes the rectangular pulse:
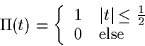
and 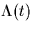 denotes the triangular pulse:
denotes the triangular pulse:
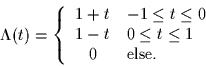
- 1.
- Compute the Fourier transform of x(t) and y(t).
- 2.
- If H(f) denotes the frequency response of the linear system, then the
relationship
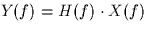 holds. Can you determine the frequency
responseH(f) of the system for all frequencies f? In particular can you
determine the response of the the system if
holds. Can you determine the frequency
responseH(f) of the system for all frequencies f? In particular can you
determine the response of the the system if 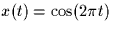 ?
?
- 3.
- Show that
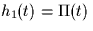 and
and 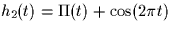 can both be
impulse responses of this system. Hence, having the response of a system to
can both be
impulse responses of this system. Hence, having the response of a system to
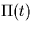 does not uniquely determine the system.
does not uniquely determine the system.
- 4.
- Does the response of an LTI system to
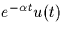 , with u(t)
denoting the unit step function, uniquely determine a system?
, with u(t)
denoting the unit step function, uniquely determine a system?
- 5.
- In general, what conditions must the input x(t) satisfy so that the
system can be uniquely determined from the output y(t)?
Prof. Bernd-Peter Paris
3/3/1998
![]()