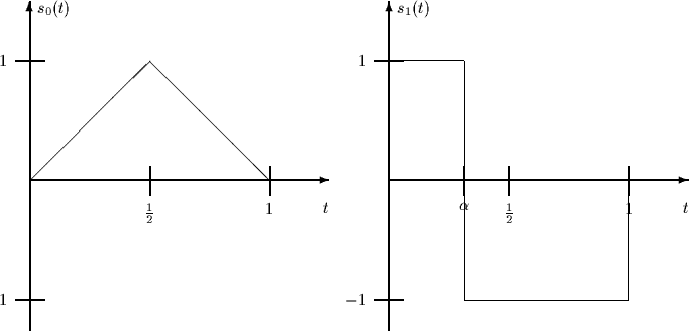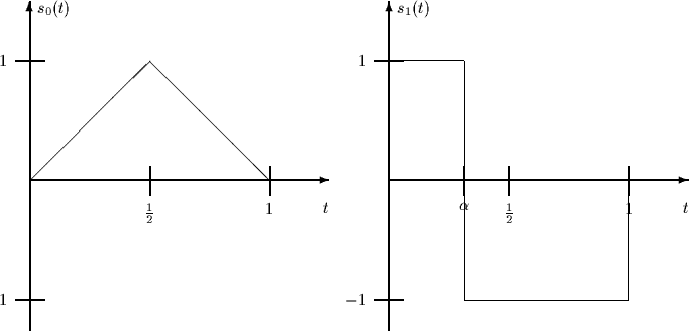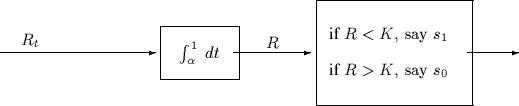Next: Linear Systems Up: Collected Problems Previous: Multi-Path Channels

Suboptimum Receiver

The following signal set is used to transmit equally likely messages over an additive white Gaussian noise channel with spectral height $\frac{N_0}{2}$ .

$\begin{picture} (450,220)(70,580) \setlength {\unitlength}{0.0125in} % \thi... ... \put(370,600){\line( 1, 0){110}} \put(480,600){\line( 0, 1){ 80}}\end{picture}$

1.: Draw and accurately label a block diagram of the optimum receiver for the above signal set.
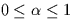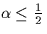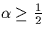2.: Compute the probability of error of the optimum receiver for $0 \leq \alpha \leq 1$ . Distinguish the cases $\alpha \leq \frac{1}{2}$ and $\alpha \geq \frac{1}{2}$ .
3.: Assume now that 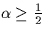$\alpha \geq \frac{1}{2}$ and that the following suboptimum receiver is used.

$\begin{picture} (100,30) \setlength {\unitlength}{1.1mm} \put(0,10){\vector... ...akebox(30,7){if $R < K$, say $s_1$}} \put(90,10){\vector(1,0){10}}\end{picture}$
Find the distribution of R for both cases, s₀(t) was transmitted and s₁(t) was transmitted.
4.: How do you have to choose the threshold K in the above receiver to minimize the probability of a bit error.
5.: Compute the resulting probability of error and compare it to the result from part (b).

Prof. Bernd-Peter Paris
3/3/1998