Linear Systems

Consider a linear system with frequency response

$$H(f) = \frac{b}{a+j 2\pi f}.$$

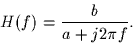
1.

Show that the impulse response of the system with the above frequency response is

$$h(t) = b \exp(-at) u(t),$$

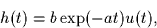
where u(t) denotes the unit step function.

2.

Determine the constant b such that the energy of the impulse response equals 1.

3.

Assume now the following signal is input to the linear system

$$x(t) = \left\{ \begin{array} {cl} 1 & \mbox{for $0 \leq t \leq T$}\\ 0 & \mbox{else.} \end{array} \right.$$

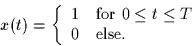
Find the output y(t) of the linear system if the signal x(t) is the input.

4.

Determine the loss of energy in the linear system, i.e., compute the difference in energy between the input signal x(t) and the output signal y(t). Use the value of b that you determined in part (b).

5.

If the input signal were triangular (instead of square) and had the same energy as x(t), would the loss of energy be different? Explain.