


Next: Coherent Reception with Imperfect
Up: Collected Problems
Previous: Problem 13
Let 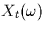 be a stochastic process defined on
be a stochastic process defined on
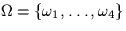 having probabibility
assignments
having probabibility
assignments
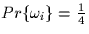 for i=1,2,3,4.
The sample functions are
for i=1,2,3,4.
The sample functions are
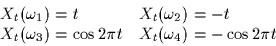
- 1.
- Compute the joint probability
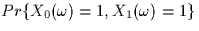 .
. - 2.
- Compute the conditional probability
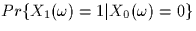 .
. - 3.
- Compute the mean and autocorrelation function of
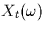 .
. - 4.
- Is this process stationary? wide-sense stationary?
Prof. Bernd-Peter Paris
3/3/1998
![]()