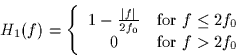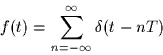Problem 13

Consider the following system

The spectrum of the input signal x₁(t) is

$$X_1(f) = \left\{ \begin{array} {cl} 1 & \mbox{for $f \leq f_0$} \\ 0 & \mbox{for $f \gt f_0$} \end{array}\right.$$

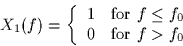
and the transfer function of the linear system S₁ is given by

$$H_1(f) = \left\{ \begin{array} {cl} 1-\frac{\vert f\vert}{2... ...f \leq 2f_0$} \\ 0 & \mbox{for $f \gt 2f_0$}\end{array}\right.$$

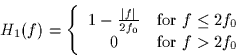
1.

Compute and sketch the spectrum of the signal y₁(t).

2.

By multiplying y₁(t) with the pulse train

$$f(t) = \sum_{n=-\infty}^{\infty} \delta(t-nT)$$

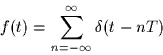
we generate the signal x₂(t). Find a condition on T such that y₁(t) can be reconstructed completely.

3.

Assume now that 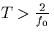$T \gt \frac{2}{f_0}$. Compute and sketch the spectrum of x₂(t).

4.

The system S₂ is used to recover the input signal x₁(t). Find the transfer function H₂(f) of S₂ such that y₂(t)=x₁(t).