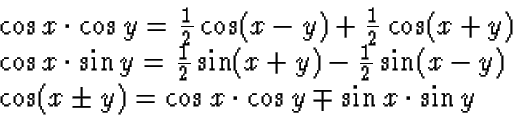AM Modulation

Throughout this problem, assume that the message signal m(t) is given as 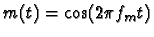$m(t)=\cos(2 \pi f_m t)$. The carrier frequency f_c is much higher than f_m.

1.

Assume m(t) is modulated using conventional DSB AM. Sketch the resulting (time-domain) signal.

2.

Compute and sketch the Fourier transform of the modulated signal.

3.

Repeat parts (a) and (b) if DSB-SC AM is used.

4.

For the remainder of the problem, assume that m(t) is input to the system in Figure 1. The cutoff frequency of the lowpass filters equals f_m. Compute x₁(t) and x₂(t) as well as their Fourier transforms X₁(f) and X₂(f).

5.

Compute the ouputs of the lowpass filters, y₁(t) and y₂(t), as well as their Fourier transforms Y₁(f) and Y₂(f).

6.

Compute the output signal s(t) and its Fourier transform S(f)

7.

How would you describe what this system does?

  

Figure 1: AM modulation

Hint: The following trigonometric identities may be useful:

$$\begin{array}{l} \cos x \cdot \cos y = \frac{1}{2} \cos(x-y)... ... y) = \cos x \cdot \cos y \mp \sin x \cdot \sin y \end{array}$$