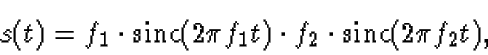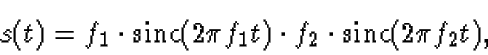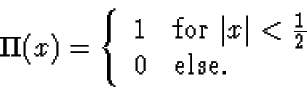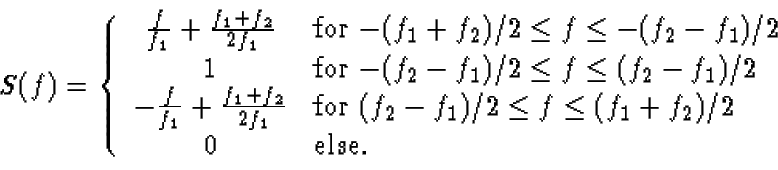Fourier Transforms

Throughout this problem consider the following signal

$$s(t) = f_1 \cdot \mbox{sinc}(2 \pi f_1 t) \cdot f_2 \cdot \mbox{sinc}(2 \pi f_2 t),$$

where $\mbox{sinc}(x) = \sin(x)/x$. Assume that f₂ > f₁. Also, let $\Pi(x)$ denote the rectangular pulse defined in class, i.e.,

$$\Pi(x) = \left\{ \begin{array}{cl} 1 & \mbox{for $\vert x\vert < \frac{1}{2}$ }\\ 0 & \mbox{else.} \end{array}\right.$$

1.

Show that the inverse Fourier transform of $\Pi(f/f_0)$ is given by $f_0 \cdot \mbox{sinc}(\pi f_0 t)$.

2.

Use the convolution rule, to find the Fourier transform S(f) of s(t). Plot the magnitude of S(f). Label your plot very accurately! What is the value of S(f₂)?

Note: If you can not solve this part of the problem you may assume for the remainder of the problem that

$$S(f) = \left\{ \begin{array}{cl} \frac{f}{f_1} + \frac{f_1 ... ...eq (f_1 + f_2)/2$ }\\ 0 & \mbox{else.} \end{array} \right.$$

3.

Is it possible to reconstruct completely the signal s(t) from samples taken at rate 1/T_s? Justify your answer! If you answered ``yes'', give the largest sampling period T_s which allows for perfect reconstruction.

4.

Now, consider the signal $r(t)= s(t) \cdot \cos(2 \pi f_2 t)$. Compute the Fourier transform R(f) of r(t). Plot the magnitude of R(f). Be very accurate!

5.

Conclude that r(t) can be written in the form $A \cdot \mbox{sinc}(2 \pi f_a t) \cdot \mbox{sinc}(2 \pi f_b t)$ with suitably selected constants A, f_a, and f_b. You must provide values for all three constants and explain how you obtained them.