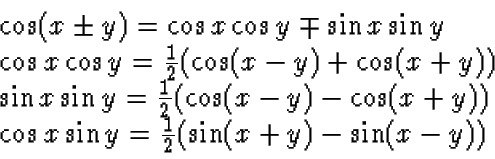Next: Linear, Time-invariant Systems
Up: Collected Problems
Previous: Throughout this problem consider
Two carriers of the same frequency but with a phase difference of 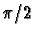 may be
used to transmit two signals simultaneously.
This is called quadrature amplitude modulation and provides the basis for the
generation of AM stereo signals. Specifically, the DSB-SC variety of such a
signal may be
described by
may be
used to transmit two signals simultaneously.
This is called quadrature amplitude modulation and provides the basis for the
generation of AM stereo signals. Specifically, the DSB-SC variety of such a
signal may be
described by
where fc is the carrier frequency and ml(t) and mr(t) are the left-hand and
right-hand message signals, respectively.
You may assume throughout that ml(t) and mr(t) are lowpass signals with bandwidth
fm much smaller than fc.
- 1.
- Draw a block diagram of a quadrature amplitude modulator, i.e., a system
with inputs ml(t) and mr(t) that
generates the signal s(t).
- 2.
- Compute the Fourier transform of the signal s(t) in terms of Mr(f) and Ml(f).
- 3.
- A ``mono'' receiver can be implemented as in the following block
diagram:
Derive an expression for the signal c(t) and then compute the Fourier
transform of the signal c(t).
- 4.
- Assume the lowpass filter to be ideal with cut-off frequency fp satisfying
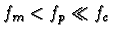 ,
find an expression for the output signal
,
find an expression for the output signal
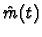 .
Explain how the mono receiver processes the received signal containing stereo
signals.
.
Explain how the mono receiver processes the received signal containing stereo
signals.
- 5.
- Propose a receiver that is capable of extracting both ml(t) and
mr(t) from s(t). Draw a block diagram of your proposed receiver and
explain in sufficient detail how and why it works.
Hint:



Next: Linear, Time-invariant Systems
Up: Collected Problems
Previous: Throughout this problem consider
Prof. Bernd-Peter Paris
2002-04-22
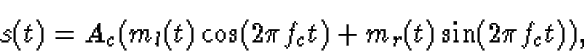
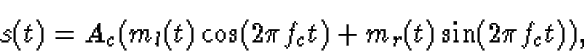
![\begin{picture}(300,120)(40,550)
\setlength{\unitlength}{0.008in} %
\thickline...
...tor( 1, 0){ 60}}
\put(280,625){\makebox(60, 0)[b]{$\hat{m}(t)$ }}
\end{picture}](img37.gif)