


Up: Collected Problems
Previous: AM Stereo
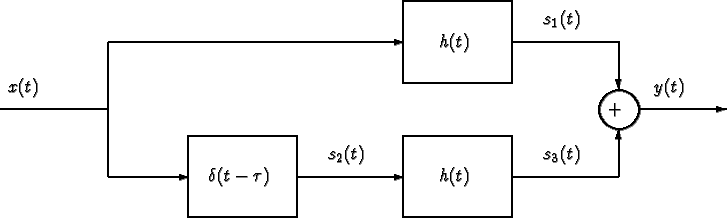
Consider the following system in which h(t) denotes the impulse response of a
linear, time-invariant system.
Throughout this problem, h(t) is given by
- 1.
- Compute the Fourier transform H(f) of h(t).
- 2.
- Assume for the remainder of the problem, that the input signal x(t) equals
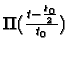 .
Assume
.
Assume
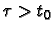 .
Determine the signal s1(t) and the Fourier transform S1(f). Plot s1(t).
.
Determine the signal s1(t) and the Fourier transform S1(f). Plot s1(t).
- 3.
- Determine the signal s2(t) and the Fourier transform S2(f). Plot s2(t).
- 4.
- Determine the signal s3(t) and the Fourier transform S3(f). Plot s3(t).
- 5.
- Compute the output signal y(t) when
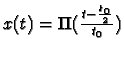 is the input. Also, compute the
Fourier transform Y(f). Plot y(t).
is the input. Also, compute the
Fourier transform Y(f). Plot y(t).
- 6.
- Determine the impulse response and frequency response of the overall
system, i.e., the system with input x(t) and output y(t).
Prof. Bernd-Peter Paris
2002-04-22

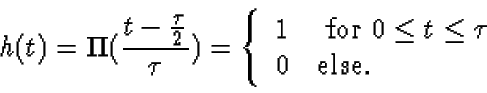
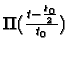 .
Assume
.
Assume
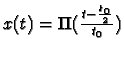 is the input. Also, compute the
Fourier transform Y(f). Plot y(t).
is the input. Also, compute the
Fourier transform Y(f). Plot y(t).