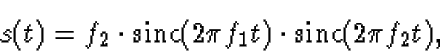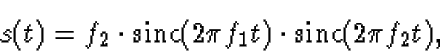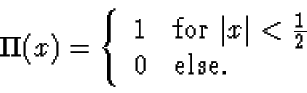Next: AM Stereo
Up: Collected Problems
Previous: Sub-Optimum Receivers
where
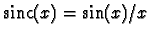 .
Assume that f2 > f1.
Also, let
.
Assume that f2 > f1.
Also, let 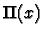 denote the rectangular
pulse defined in class, i.e.,
denote the rectangular
pulse defined in class, i.e.,
- 1.
- Show that the inverse Fourier transform of
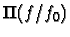 is
given by
is
given by
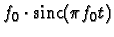 .
.
- 2.
- Use the convolution rule, to find the Fourier transform S(f) of s(t).
Plot the magnitude of S(f). Be very accurate!
- 3.
- Is it possible to completely reconstruct the signal
s(t) from samples taken at rate 1/Ts?
Justify your answer!
If you answered ``yes'',
give the largest sampling period Ts which allows for perfect reconstruction.
- 4.
- Now, consider the signal
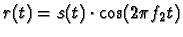 .
Compute
the Fourier transform R(f) of r(t). Plot the magnitude of R(f). Be
very accurate!
.
Compute
the Fourier transform R(f) of r(t). Plot the magnitude of R(f). Be
very accurate!
- 5.
- Conclude that r(t) can be written in the form
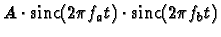 with
suitably selected constants A, fa, and fb. You must provide values
for all three constants and explain how you obtained them.
with
suitably selected constants A, fa, and fb. You must provide values
for all three constants and explain how you obtained them.
Prof. Bernd-Peter Paris
2002-04-22