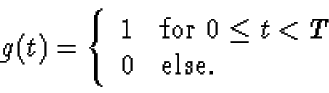Next: Throughout this problem consider
Up: Collected Problems
Previous: M-ary Signal Sets
A binary communication system employs the following signals to
communicate two equally likely messages over an additive white Gaussian
noise channel with spectral height
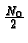 :
:
- 1.
- Draw a block diagram of the optimum receiver.
- 2.
- Compute the probability of error achieved by your receiver from
part (a).
- 3.
- Consider now the following suboptimum receiver:
where g(t) is given by
Find the distribution of R for both cases, s0(t) was transmitted
and s1(t) was transmitted.
- 4.
- Find the probability of error of the suboptimum receiver and
compare with that of the optimum receiver.
- 5.
- If
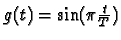 were used in the sub-optimum receiver,
would the resulting probability of error be larger or smaller than
the probability of error achieved with the g(t) in part (c)? Explain.
were used in the sub-optimum receiver,
would the resulting probability of error be larger or smaller than
the probability of error achieved with the g(t) in part (c)? Explain.
Prof. Bernd-Peter Paris
2002-04-22
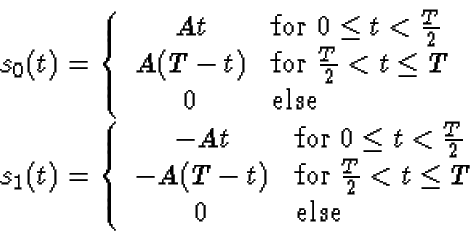
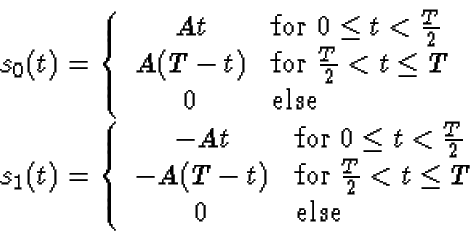
![\begin{picture}(100,30)
\setlength{\unitlength}{1mm}
\put(0,10){\vector(1,0){12...
...90,10){\vector(1,0){10}}
\put(98,11){\makebox(0,0)[b]{$\hat{b}$ }}
\end{picture}](img24.gif)