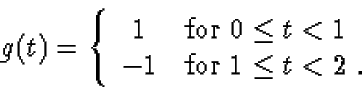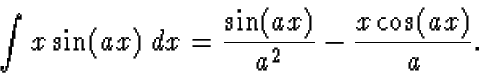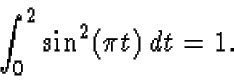Mismatched Filters

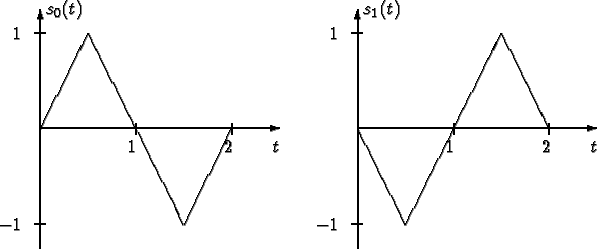
The following signal set is employed to transmit equally likely signals over an additive white Gausssian noise channel with spectral height $\frac{N_0}{2}$.

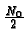1.

Sketch and accurately label the block diagram of the receiver which minimizes the probability of error.

2.

Compute the probability of error of your receiver from part (a).

3.

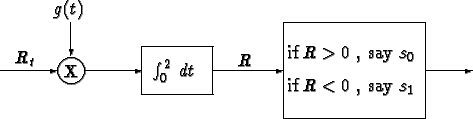
Consider now the following receiver:

Compute the probability of error of this receiver if $g(t) = \sin(\pi t)$.

4.

Repeat part (c) for

$$g(t) = \left\{ \begin{array}{cl} 1 & \mbox{for $0 \leq t < 1$ }\\ -1 & \mbox{for $1 \leq t < 2$ .} \end{array} \right.$$

5.

Compare the probabilities of error in parts (b)-(d). Which probability of error is largest? Which is smallest? Explain.

Hint: You may need

$$\int x \sin(ax)\;dx = \frac{\sin(ax)}{a^2} - \frac{x \cos(ax)}{a}.$$

$$\int_0^2 \sin^2(\pi t) \; dt = 1.$$