


Next: M-ary Signal Sets
Up: Collected Problems
Previous: Mismatched Filters
The following signal set is used to transmit equally likely messages
over an additive white Gaussian noise channel with spectral height
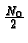 :
:
- 1.
- Draw a block diagram of the receiver which achieves the minimum
probability of error for this signal set. Be sure to specify the value of
the threshold.
- 2.
- What is the minimum probability of error achievable with this signal set?
- 3.
- Consider the following receiver, where
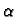 is a positive constant.
Determine the distribution of the random variable R as a function of
is a positive constant.
Determine the distribution of the random variable R as a function of 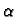 for both cases, s0(t) was
transmitted and s1(t) was transmitted.
Sketch the two density functions and indicate the location of the threshold.
for both cases, s0(t) was
transmitted and s1(t) was transmitted.
Sketch the two density functions and indicate the location of the threshold.
- 4.
- Compute the probability of error achieved by this receiver as a
function of the constant
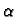 .
.
- 5.
- For what value of
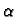 is the probability of error
minimized? Compare with the result from part (b).
is the probability of error
minimized? Compare with the result from part (b).
Prof. Bernd-Peter Paris
2002-04-22
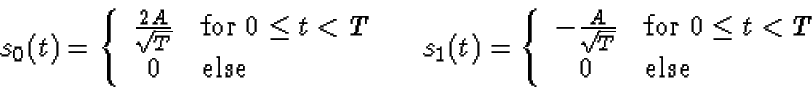
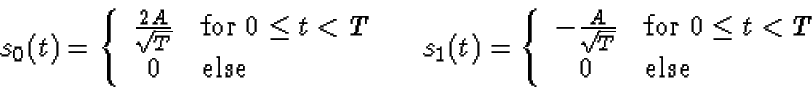
![\begin{picture}(100,30)
\setlength{\unitlength}{1mm}
\put(0,10){\vector(1,0){...
...0,10){\vector(1,0){10}}
\put(98,11){\makebox(0,0)[b]{$\hat{b}$ }}
\end{picture}](img18.gif)