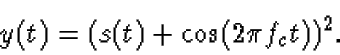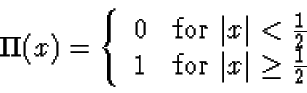AM Modulator

In this problem, we are investigating an alternative method for generating an AM signal that does not require the use of a multiplier.

Throughout this problem, assume that s(t) is a band-limited signal, i.e., the Fourier transform S(f) of the signal s(t) equals zero for frequencies higher than some f₀: S(f)=0 for |f|>f₀. Further, the frequency f_c is much larger than f₀.

1.

Find the Fourier transform of the signal

$$y(t)=(s(t) + \cos(2\pi f_c t))^2.$$

It is probably best if you begin by expanding the square in the expression for y(t).

2.

Compute and sketch the magnitude of the Fourier transform Y(f) for the case $S(f)=\Pi(f/f_0)$.

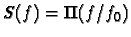3.

Now assume that s(t) = A +m(t), where m(t) is a band-limited (to f₀) message signal. Compute the Fourier transform Y(f) for this case.

4.

Now let y(t) be the input to a bandpass filter. Determine the cut-off frequencies of the filter such that the output of the bandpass is an AM signal.

5.

Draw a block diagram of a non-coherent AM demodulator.

Reminder:

$$\Pi(x) = \left\{ \begin{array}{cl} 0 & \mbox{for $\vert x\v... ...box{for $\vert x\vert \geq \frac{1}{2}$ } \end{array} \right.$$