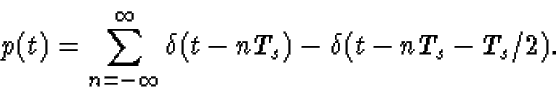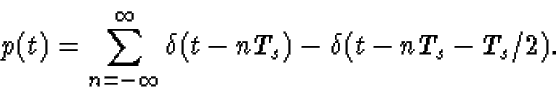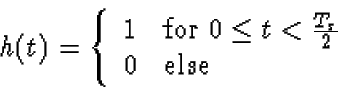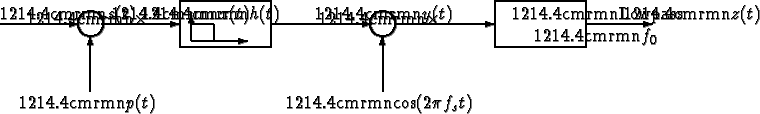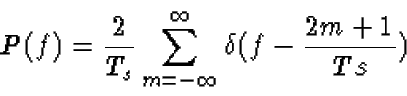Sampling System

Throughout this problem, the system in the diagram below is considered. The signal p(t) is a sequence of ideal pulses (delta functions), specifically

$$p(t) = \sum_{n=-\infty}^\infty \delta(t-nT_s) - \delta(t-nT_s - T_s/2).$$

Assume throughout that the signal s(t) is band-limited, i.e., the Fourier transform S(f) of the signal s(t) equals zero for frequencies higher than some f₀: S(f)=0 for |f|>f₀. Further, the frequency f_s=1/T_s is much larger than f₀. The impulse response h(t) of the first filter is given by

$$h(t) = \left\{ \begin{array}{cl} 1 & \mbox{for $0 \leq t < \frac{T_s}{2}$ }\\ 0 & \mbox{else} \end{array} \right.$$

#1#2#3#4#5 @font#1#2pt #3#4#5

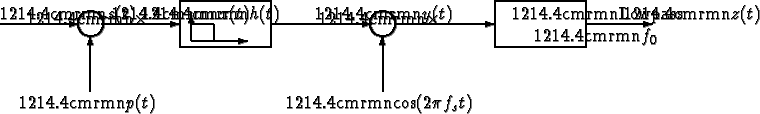
1.

Sketch the signal p(t).

2.

Compute the Fourier transform of p(t). If you can not solve this problem, you may assume that

$$P(f) = \frac{2}{T_s} \sum_{m=-\infty}^\infty \delta(f-\frac{2m+1}{Ts})$$

for the remainder of the problem.

3.

Compute the Fourier transform X(f) of x(t).

4.

For a ``typical'' input signal s(t), sketch the signal y(t) at the output of the first filter.

5.

Compute the Fourier transform Y(f) of y(t).

6.

Explain under which conditions the output signal z(t) will be approximately equal to the input signal s(t). Be as specific as you can.