Sharing a secret

• If two parties communicate regularly they can simply agree on values A, B, N, X(0) (using secure communications, such as a personal meeting or a trusted messenger).
• However, if no prior relationship exists parameters A, B, N, X(0) must be agreed upon before encryption can be used.
• Clearly, simply transmitting values A, B, N, X(0) does not lead to a secure situation. An eavesdropper can intercept the parameters and then decryp t the message.
• A solution to this dilemma is provided by public key cryptography.
• Example: Receiver R and transmitter T want to establish an encrypted cmmunications channel.
• R says:
  • Send me parameters A, B, and N unencrypted.
  • Instead of sending the seed X(0), compute the remainder C when X(0)^eis divided by n. (For this example X(0) would have to be between 0 and 32.)
  • Then, send me C.
• E.g., if the transmitter selected X(0)=5, and e=3, n=33. Then 5³=125 and the remainder when divided by 33 is C=26.
• Only the receiver can then find X(0) by computing the remainder when C^d is divided by n.
• The exponent d is very difficult to guess from e and n.
• Here d=7; the receiver computes 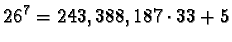$26^7=243,388,187 \cdot 33 + 5$. Thus, the remainder equals 5.
• Now encryption can begin as both R and T know parameters A, B, N, X(0).
• An eavesdropper has only seen C and does not know d. Hence, he can not recover X(0).