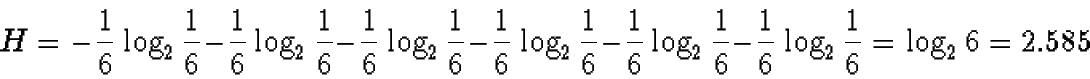Example: Rolling a die

• Assume that a fair die is rolled and the result is to be represented in binary form.
• The entropy for this problem is
  
  $$H= -\frac{1}{6}\log_2 \frac{1}{6} - \frac{1}{6}\log_2 \frac{1... ...rac{1}{6} - \frac{1}{6}\log_2 \frac{1}{6} = \log_2 6 = 2.585$$
  
  

• Using a Huffman tree, the following binary representation can be determined
  

  Number	Binary representation
  1	00
  2	01
  3	100
  4	101
  5	110
  6	111
  Average Number of bits:	2.66

• This example demonstrates the typical case when the average number of bits is larger than the entropy.
• With a Huffman code, the average number of bits is always between H and H+1.
• The efficiency of the representation can be improved if several rolls of the die are coded simultaneously.
• For example, when two rolls of the die are combined 36 equally likely combinations arise.
• The entropy for this case doubles to 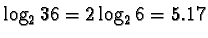$\log_2 36 = 2\log_2 6 = 5.17$ bits.
• The average number of bits via Huffman coding is 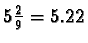$5 \frac{2}{9} = 5.22$ bits.
• The difference between entropy and number of bits in the shortest possible binary representation vanishes as more rolls of the die are combined.