[prev] [prev-tail] [tail] [up]

Homework 5 (Due: December 4)

[PDF]

ECE 732: Mobile Communication Systems
Prof. B.-P. Paris
Homework 5
Due: December 4, 2018

Suggested Reading:
Goldsmith: Chapter 11
Problems
  1. Problem 11.2 in Goldsmith
  2. Maximum Likelihood Sequence Estimation
    A binary sequence of five symbols x (elements are drawn from xn ∈ {-1, 1}) is transmitted over a channel which is characterized by a tapped delay-line with coefficients a = -2 and b = 3. Remember that the output sequence will have six samples; also assume that the register is initially loaded with a ’0’. The observation is further corrupted by real-valued, additive white Gaussian noise.

    The following sequence r is observed at the output of the tapped delay line

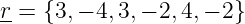
    r-= {3,- 4,3,- 2,4,- 2}

    SVG-Viewer needed.

    1. Given the observed sequence r, determine the most likely input sequence x. Show clearly how you arrived at your solution.
    2. Draw and clearly label a trellis diagram and indicate the path through the trellis which corresponds to the most likely sequence.
    3. What is the Euclidean distance associated with the two sequences x1 = {-1, 1,-1, 1,-1} and x2 = {-1, 1, 1, 1,-1}, respectively? Explain what this implies about the decisions by the Viterbi equalizer.
  3. Retrieve the MATLAB function tdl.m. Explain in your own words what it does.
  4. Generate a BPSK signal sampled once per bit period and use it as the input /Users/pparis/Home/Courses/ece732/I to tdl.m. For f=[1], f=[0.7 0.7*i], and f=[0.5 0.7*i 0.5], plot the real part of the output versus the imaginary part of the output. Vary the noise variance var between 0 and 1.
    What do you observe? What is the significance of what you are observing?
    In one of your plots, indicate the decision boundary of the receiver that ignores ISI. How would that matched filter perform if you applied it to the the different output signals.
  5. Repeat Problem 2 with a QPSK signal.
  6. Retrieve the MATLAB function va.m which implements the Viterbi algorithm for maximum-likelihood sequence estimation in the presence of intersymbol interference. Inputs to the function are a vector of observations, the coefficients of the tapped delay line model, and a list of the possible values that the digital sequence to be estimated can assume. Outputs are the estimated sequence and the mean-square error between the observation and the convolution of the estimated sequence and the filter coefficients.
    Experiment with this function under a variety of conditions using tdl.m.
    Note: va.m requires the following auxiliary functions:

[prev] [prev-tail] [front] [up]