In realistic communication systems, the amplitude of signals in a signal set used for digital communication may be known by the transmitter but are usually scaled by an unknown amount prior to reception. Performance can become poor when the received signals are small and are contaminated by additive white Gaussian noise.
Assume that a binary, orthogonal signal set having equally likely,
equal energy components is chosen for this channel.
The received signal is of the form
where
- Find the minimum probability of error receiver for this signal set.
- A clever engineer wants to estimate the unknown amplitude
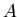 by
evaluating
by
evaluating
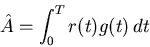
when the signal is present.
What single choice for
is present.
What single choice for  both
both
- minimizes the percentage error of the estimate as expressed by the coefficient of variation (defined as the ratio of the standard deviation of the estimate to its mean) and
- results in an unbiased estimate, i.e.,
![$E[\hat{A}] = A$](img162.png) .
.
- The engineer decides that the receiver should ``shut off'' when
the estimate of
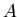 suggests that errors are occurring too frequently.
What threshold value for
suggests that errors are occurring too frequently.
What threshold value for 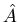 should be used in an attempt to
guarantee that the error rate is less than
should be used in an attempt to
guarantee that the error rate is less than 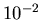 .
Assume
.
Assume 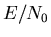 equals unity in this part.
equals unity in this part.
For those who remember the days of the bandwagon, the secret to the Washington Redskins success in the 1991/92 season was the installation of a new digital communication system for relaying messages from the press box to the field. A former ECE 630 student designed the following binary signal set:
The duration of each transmission interval is
- What is the minimum probability of error that any receiver can achieve when this presumably well designed communication system is used.
- When visiting RFK stadium, the Houston Oilers decided to jam this system and nearly managed to beat the Redskins.
(I know this was a long time ago, but you may recall that they missed the
game-winning field goal with time running out.)
What they did is to transmit a constant amplitude cosine wave of
frequency
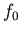 .
In the presence of this jammer, the received signal can be modeled as
.
In the presence of this jammer, the received signal can be modeled as
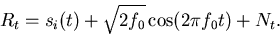
The noise has the same characteristics as described above. What is the probability of error when the receiver from part (a) is used. - In this game, the famous Redskins' half-time adjustments included a redesign of the receiver for the communication system. Find the optimum receiver for communication in the presence of the jamming signal and the corresponding probability of error.
- The (then lowly) Dallas Cowboys on their visit to RFK stadium used a
smarter
jammer.
They transmitted a cosine wave whose amplitude alternates between
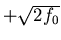 and
and 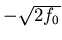 .
This jamming signal has a fixed amplitude over each signalling
interval and the amplitude is equally likely to be positive or
negative.
Assuming the sign of the jamming signal during a particular
transmission interval is statistically independent of the sign in any
other interval and the noise characteristic is as before, explain why
the Cowboys brought the Redskins winning streak to an end despite all
efforts to adjust at halftime.
.
This jamming signal has a fixed amplitude over each signalling
interval and the amplitude is equally likely to be positive or
negative.
Assuming the sign of the jamming signal during a particular
transmission interval is statistically independent of the sign in any
other interval and the noise characteristic is as before, explain why
the Cowboys brought the Redskins winning streak to an end despite all
efforts to adjust at halftime.
Diversity signalling is the transmission of the same message over
Assume that an on-off signalling scheme is used over each of N Rayleigh
channels. The received signals are of the form:
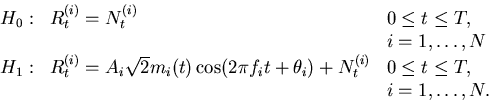
The amplitude
- Find the optimum receiver which uses the output of only one channel.
- Find the optimum receiver which uses the output of all channels.
- Find an expression for the probability of error when the
hypotheses are equally likely for each receiver.
Warning: This problem is very hard. - Compare the results for the first receiver (
 ) and the
second receiver (
) and the
second receiver ( ).
Does diversity signalling result in improved performance?
).
Does diversity signalling result in improved performance?
Artificial Neural Networks are being explored in a variety of problem areas. In this problem we will demonstrate that a neural network can be used as a vector receiver in communication applications. (An important feature of neural networks is their ``learning'' ability, which we do not consider here.)
In a vector communication problem, the vector receiver observes a
vector ![]() of
of ![]() random variables and tries to determine which of several hypotheses,
random variables and tries to determine which of several hypotheses,
![]() , is
most likely to have produced this observation.
, is
most likely to have produced this observation.
The fundamental element of artificial neural networks is the neuron, typically depicted as:
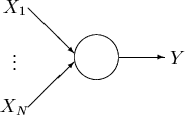
A neuron receives ![]() inputs
inputs
![]() and yields the single
output
and yields the single
output ![]() by computing
by computing
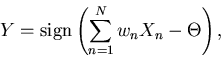
where
- Find the optimum set of weights and threshold used by a neuron
to distinguish between equally likely signals,
 and
and
 , when they are presented to the neuron in additive
Gaussian noise with uncorrelated components.
, when they are presented to the neuron in additive
Gaussian noise with uncorrelated components.
- One problem with neural networks is unknown signal amplitudes: they can be sensitive to scaling. Under what conditions will the single neuron be insensitive to the size of the signal?
- How can an optimum receiver for ternary signal sets be constructed from neurons? Hint: You will have to interconnect neurons into layers. The first layer is responsible for distinguishing between each possible pair of hypotheses and the second layer combines the results from the first layer.
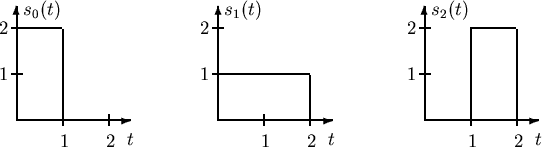
The channel adds white Gaussian noise of spectral height
![]() to the transmitted signal.
to the transmitted signal.
- Draw and accurately label a block diagram of the optimum receiver, i.e., the receiver that minimizes the probability of a wrong decision.
- Find the appropriate signal space and indicate the decision regions of the optimum receiver.
- Compute the minimum probability of error attainable with this signal set.
- Repeat part (b) under the assumption that the amplitude of
signal
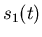 is increased to
is increased to 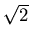 .
.
- Find another signal set with
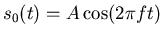 that achieves the same performance as the signal set sketched above.
that achieves the same performance as the signal set sketched above.
The following signal set is used to transmit equally likely messages over an additive white Gaussian noise channel with spectral height
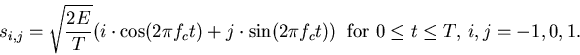
Thus, this signal set consists of
- Draw and accurately label the signal constellation in an appropriately chosen signal space and indicate the decision boundaries formed by the optimum receiver.
- Compute the probability of error achieved by the optimum receiver.
- Assume that the energy of the transmitted signal can never
exceed
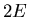 . Is it possible to modify the above signal set in such a
way that the probability of error is reduced without exceeding the
limit on the signal energy? Explain why or why not.
. Is it possible to modify the above signal set in such a
way that the probability of error is reduced without exceeding the
limit on the signal energy? Explain why or why not.
The following signal set is used to transmit equally likely messages over an additive white Gaussian noise channel with spectral height
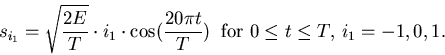
Thus, this signal set consists of
- Draw and accurately label a block diagram for the optimum receiver for this signal set.
- Draw and accurately label the signal constellation in an appropriately chosen signal space and indicate the decision boundaries formed by the optimum receiver. Then, compute the probability of error achieved by the optimum receiver.
- Repeat part (b) for the following signal set
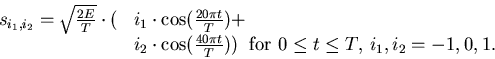
- Repeat part (b) for the following signal set
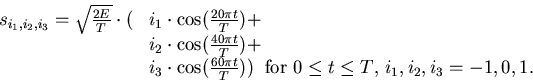
- Derive a general expression for the probability of error of the
N-dimensional signal set
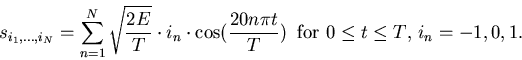
The following signal set is used to transmit equally likely messages over an additive white Gaussian noise channel with spectral height
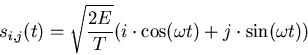
for
- Draw and accurately label the signal constellation in an appropriately chosen signal space and indicate the decision boundaries formed by the optimum receiver.
- Compute the probability of error achieved by the optimum receiver.
- Assume now that signal
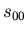 is removed from the above signal
set. Draw and accurately label the new signal constellation in an
appropriately chosen signal space and indicate the new optimum
decision boundaries.
is removed from the above signal
set. Draw and accurately label the new signal constellation in an
appropriately chosen signal space and indicate the new optimum
decision boundaries.
- Can you still express the resulting probability of error in terms of the Q-function? If your answer is yes, compute the probability of error; if it is no, explain why not and indicate whether the probability of error of the reduced signal set is larger or smaller than that of the original set.