- Random Amplitude
Let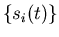 ,
,
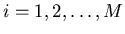 denote the signals
comprising a transmitter's signal set.
This set is said to be an
orthogonal signal set if the signals are pairwise orthogonal,
denote the signals
comprising a transmitter's signal set.
This set is said to be an
orthogonal signal set if the signals are pairwise orthogonal,
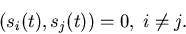
Usually, the signals in an orthogonal signal set have equal energies,
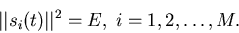
Under these conditions and assuming the members of the set are equally likely, solve the following problems.- Sketch a block diagram of the minimum probability of error receiver when the channel adds white Gaussian noise to the transmitted signal.
- Now assume the channel introduces a random amplitude
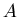 during
transmission.
How does the receiver from part (a) have to be modified to accommodate
this channel if the density of
during
transmission.
How does the receiver from part (a) have to be modified to accommodate
this channel if the density of 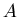 is one sided exponential,
is one sided exponential,
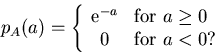
- Find an expression for the probability of error of your receiver.
- Repeat parts (b) and (c) for the case when the distribution of
the amplitude
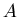 is Gaussian with zero mean and unit variance.
is Gaussian with zero mean and unit variance.
- Digital Interference
One potential problem in digital communication is interference from other digital transmitters as well as from the channel noise. Assume that transmitter A is using signal set A,
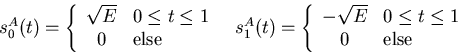
and transmitter B uses signal set B,
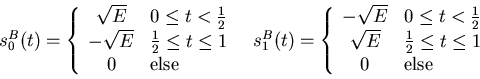
Assume the signals in each set are equally likely. The receiver trying to pay attention to transmitter A receives the signal
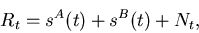
where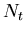 is white Gaussian noise.
Assume that the transmitters A and B are synchronized so that the bit
intervals coincide.
The signals sent by each transmitter are statistically independent.
is white Gaussian noise.
Assume that the transmitters A and B are synchronized so that the bit
intervals coincide.
The signals sent by each transmitter are statistically independent.
- Determine the minimum probability of error receiver for the reception of transmitter A's signals in this situation.
- What is the resulting probability of error in this situation?
- How does your answer for part (a) change if if transmitter B
uses the signal set
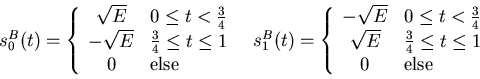
Sketch decision regions in the signal space spanned by and
and  .
.
- Binary Phase Channel
A modulated antipodal signal set is used over a channel which changes the phase of the transmitted signal by or leaves the
phase unchanged.
This phase shift changes randomly from bit-to-bit and is equally
likely to occur or not.
The transmitted signals are equally likely to occur.
or leaves the
phase unchanged.
This phase shift changes randomly from bit-to-bit and is equally
likely to occur or not.
The transmitted signals are equally likely to occur.
- Find the optimum receiver for this channel.
- Calculate the resulting probability of error for your receiver.
- Channel Measurement Signal Sets
One method of communicating over a channel in which parameters vary slowly compared with a bit interval is to precede the information-bearing portion of the bit interval with a known probe signal. This signal can then be used to provide some information about the channel which can be used to aid in the detection problem.Assume a modulated signal set is used over a random phase channel. The baseband probe signal
 is always transmitted over the
first half of the bit interval.
The baseband message signal
is always transmitted over the
first half of the bit interval.
The baseband message signal 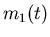 is used to transmit
equally-likely information in the second half.
The received signal is of the form.
is used to transmit
equally-likely information in the second half.
The received signal is of the form.
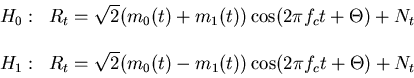
where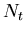 is white Gaussian noise and
is white Gaussian noise and 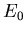 and
and 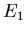 , the energies
of probe and message signals, are equal.
, the energies
of probe and message signals, are equal.
- Assume the phase
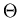 is a known constant.
Show that the optimum receiver ignores the probe portion of the
received signal.
is a known constant.
Show that the optimum receiver ignores the probe portion of the
received signal.
- Now assume that
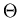 is a random variable uniformly
distributed over the interval
is a random variable uniformly
distributed over the interval 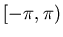 .
Find the minimum probability of error receiver.
.
Find the minimum probability of error receiver.
- Show that this receiver can be put in the form of a phase
discriminator where the phases of the probe and message portions of
the received signal are compared.
The discriminator announces
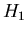 if the phase difference is greater
than
if the phase difference is greater
than  in magnitude and
in magnitude and 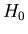 otherwise.
otherwise.
- Find the probability of error of the optimum receiver.
- How does the performance of this signal set compare with that when no probe signal is used?
- Assume the phase