Homework 9 (Due: November 14)

[PDF]

Reading

Madhow:

1. Chapter 5: especially sections 5.6-5.8.

Problems

1. Gray Coding
   In class we discussed that constellations with M symbols can be used to transmit R = log ₂M bits per symbol. Put differently, we can organize a sequence of bits into groups of R and map each such group to one of the M = 2^R symbols. However, we did not discuss how we should map groups of bits to symbols.

   It is very desirable that symbols in our constellation that are closest together differ in only one bit position. For example, for a QPSK constellation, the following mapping from bits to symbols is preferred:

   Bits	Symbol
   00	1 + j
   01	-1 + j
   11	-1 - j
   10	1 - j

   With this mapping, symbols that are at distance d_min = 2 from each other (e.g., symbols 1 + j and 1 - j) all differ in exactly one bit. Symbols that are at distance d = 2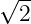 from each other (e.g., symbols 1 + j and -1 - j) differ in both bit positions.

   1. Draw a constellation diagram for QPSK (IQ plot showing the four constellation points) and annotate each constellation point with the above bit pattern. Mark up all pairs of symbols separated by d_min = 2 and verify that all pairs differ by one bit.
   2. Design a mapping from groups of 3 bits to 8-PSK symbols such that adjacent symbols differ in exactly one bit position. Illustrate your mapping using a constellation plot.
   3. Design a mapping from groups of 4 symbols to 16-QAM symbols. such that all symbol pairs separated by distance d_min = 2 differ in exactly one bit position. Illustrate your mapping using a constellation plot.
2. Madhow: Problem 5.4
3. Madhow: Problem 5.5
4. Madhow: Problem 5.35