Channel Correlation Functions Consider a WSSUS channel with scattering function

$$\Psi_S(\tau, \nu) = \Psi_1(\tau) \cdot \Psi_2(\nu),$$

where

$$\Psi_1(\tau) = \left\{ \begin{array}{cl} 1 & \mbox{for $0 \leq \tau \leq T_m$}\\ 0 & \mbox{else} \end{array} \right.$$

and

$$\Psi_2(\nu) = \left\{ \begin{array}{cl} \frac{1}{f_m} (1-(... ...t\nu\vert \leq f_m$}\\ 0 & \mbox{else.} \end{array} \right.$$

1. Find the Power Delay Profile $\Psi_g(\tau)$.
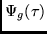2. Determine the Doppler PSD $\Phi_H(\nu)$.
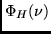3. Compute the mean delay 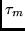$\tau_m$ and the delay spread $\sigma_{\tau}$.
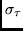4. Compute the Doppler spread $\sigma_{\nu}$.
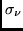5. What are the coherence time and coherence bandwidth?