Time-Varying Channels

A wireless channel is specified by the time-varying channel impulse response

$$g(t,\tau) = 1 \cdot \cos(2\pi f_d t) \mbox{, for $0 \leq \tau \leq T$}.$$

1. Determine the time-varying channel transfer function $T(f,t)$.
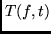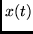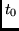2. Compute the output of the channel when the input $x(t)$ is an impulse at time $t_0$, i.e., compute the response to the signal
   
   $$x(t) = \delta(t-t_0).$$
   
   

3. What is the output when the input is a constant signal
   
   $$x(t) = 1 \mbox{, for all $t$}?$$
   
   

4. What is the output when the input is
   
   $$x(t) = \left\{ \begin{array}{cl} 1 & \mbox{for $0 \leq t \leq T$}\\ 0 & \mbox{else?} \end{array} \right.$$