


Next: Reconstruction of Sampled Signals
Up: Collected Problems
Previous: M-ary Signal-Set
The message signal m(t) is input to the system shown in the block diagram
below.
The message signal is strictly band-limited, i.e., M(f)=0 for
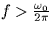 .
Furthermore, the frequency
.
Furthermore, the frequency 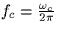 is much larger than the
highest signal frequency:
is much larger than the
highest signal frequency: 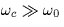 .The lowpass filters are assumed to be ideal and have cut-off frequencies equal
to the highest signal frequency.
.The lowpass filters are assumed to be ideal and have cut-off frequencies equal
to the highest signal frequency.
![\begin{picture}
(400,180)(20,620)
\setlength {\unitlength}{0.0125in}
%
\thick...
...akebox(40,0)[b]{$z_2(t)$}}
\put(380,712){\makebox(40,0)[b]{$s(t)$}}\end{picture}](img36.gif)
- 1.
- Compute the Fourier transforms of the signals x1(t) and x2(t) as a
function of the Fourier transform M(f) of the message signal.
Sketch the two resulting Fourier transforms assuming a typical spectrum
M(f).
Be careful and consider that the Fourier transforms are complex valued!
- 2.
- Describe and quantify the effect of the low pass filters: give an
expression for the Fourier transforms of the signals y1(t) and y2(t) and
sketch the two resulting Fourier transforms assuming a typical spectrum
M(f).
- 3.
- Compute the Fourier transforms of the signals z1(t) and z2(t).
Then, sketch the two resulting Fourier transforms assuming a typical spectrum
M(f).
- 4.
- Compute the spectrum of the signal s(t) and sketch it assuming a typical spectrum
M(f).
- 5.
- What happens if s(t) is multiplied with
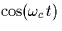 and then
passed through an ideal lowpass filter with cut-off frequency
and then
passed through an ideal lowpass filter with cut-off frequency 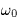 ?
?
- 6.
- Explain how the circuit above can be used in a communication system.



Next: Reconstruction of Sampled Signals
Up: Collected Problems
Previous: M-ary Signal-Set
Prof. Bernd-Peter Paris
3/3/1998
![\begin{picture}
(400,180)(20,620)
\setlength {\unitlength}{0.0125in}
%
\thick...
...akebox(40,0)[b]{$z_2(t)$}}
\put(380,712){\makebox(40,0)[b]{$s(t)$}}\end{picture}](img36.gif)
![\begin{picture}
(400,180)(20,620)
\setlength {\unitlength}{0.0125in}
%
\thick...
...akebox(40,0)[b]{$z_2(t)$}}
\put(380,712){\makebox(40,0)[b]{$s(t)$}}\end{picture}](img36.gif)