


Next: Binary Transmission in the
Up: Collected Problems
Previous: Sub-optimum Receivers
Consider an amplitude modulated signal x(t) in which the carrier's phase
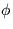 is not equal to zero, i.e.,
is not equal to zero, i.e.,
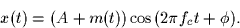
You may assume throughout the problem that the highest frequency fm in
the message signal is much smaller than the carrier frequency fc and
that the constant A has been chosen such that (A+m(t)) > 0 for all t.
- 1.
- Find the Fourier transform X(f) of the transmitted signal x(t) in terms of
of the Fourier transform M(f) of the message signal m(t).
- 2.
- Consider the following receiver front-end.
The lowpass filters are assumed to be ideal and have cut-off frequencies fm.
Find the Fourier transform of the signals y1(t) and y2(t).
- 3.
- Draw the detailed block-diagram of a system which
- takes inputs y1(t) and y2(t),
- produces a signal proportional to A+m(t),
- does not assume knowledge of the phase
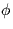 ,
, - but works reliable for all possible values of
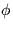 .
.
Explain why your design will meet the above criteria.
- 4.
- Give an alternate receiver block-diagram, which does not involve any
multipliers and demodulates the AM-signal reliably for all values of the
unknown phase
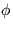 .
.
Hint: The following identities may be useful:
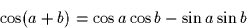
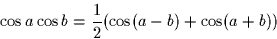
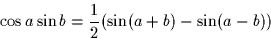



Next: Binary Transmission in the
Up: Collected Problems
Previous: Sub-optimum Receivers
Prof. Bernd-Peter Paris
3/3/1998
![]() is not equal to zero, i.e.,
is not equal to zero, i.e.,
![]()
![\begin{picture}
(300,241)(20,580)
\setlength {\unitlength}{0.0125in}
%
\thick...
...ebox(60,0)[b]{$y_1(t)$}}
\put(260,670){\makebox(60,0)[b]{$y_2(t)$}}\end{picture}](img19.gif)
![]()
![]()
![]()