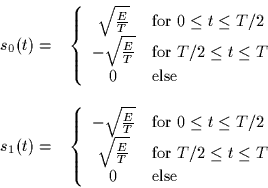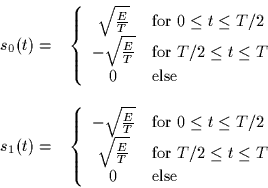Up: Collected Problems
Previous: Non-Ideal Channels
The following binary signal set is used to transmit equally likely
messages over an additive white Gaussian noise channel (spectral
height 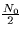 ),
),
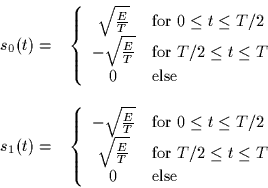
- 1.
- Draw a block diagram of the optimum receiver
which uses only a single correlator.
- 2.
- Compute the
probability of error for this receiver.
- 3.
- Assume now that the receiver is not properly synchronized with the
received signals.
Specifically, the signals are subject to a an unknown delay
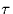 during
transmission.
Hence, the received signals is
during
transmission.
Hence, the received signals is 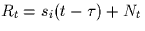 , with i=0 or 1, but
the receiver still correlates with s0(t)-s1(t).
Find the probability of error as a function of the delay error
, with i=0 or 1, but
the receiver still correlates with s0(t)-s1(t).
Find the probability of error as a function of the delay error 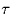 .
. - 4.
- For which value of of the delay
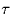 does the probability of error
become 50%?
does the probability of error
become 50%?
Prof. Bernd-Peter Paris
3/3/1998