


Next: Binary Signal Sets
Up: Collected Problems
Previous: Reconstruction of Sampled Signals
Consider an amplitude modulated signal x(t) in which the carrier's phase
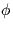 is not equal to zero, i.e.,
is not equal to zero, i.e.,
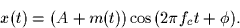
You may assume throughout the problem that the highest frequency fm in
the message signal is much smaller than the carrier frequency fc and
that the constant A has been chosen such that (A+m(t)) > 0 for all t.
- 1.
- Find the Fourier transform X(f) of the transmitted signal x(t) in terms of
of the Fourier transform M(f) of the message signal m(t).
- 2.
- Consider first the coherent demodulator in the following block diagram
Notice, that the demodulator is ``unaware'' of the phase-offset
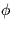 in
the modulator!
Find an expression for the Fourier transform Y(f) of the signal y(t).
in
the modulator!
Find an expression for the Fourier transform Y(f) of the signal y(t).
- 3.
- Assuming that the lowpass is ideal with cut-off frequency fm,
find an expression for the output signal z(t).
How does the phase-offset affect coherent demodulation?
- 4.
- For the remainder of the problem,
consider a non-coherent demodulator of the following form
The subsystems labeled
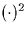 and
and 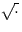 take the square and
square-root of their respective inputs.
take the square and
square-root of their respective inputs.
Find an expression for the Fourier transform of the signal x2(t)
in terms of the Fourier transform M(f) of the message signal m(t).
- 5.
- Assuming that the Fourier transform M(f) of the message signal m(t) is
given by
![[*]](http://thalia.spec.gmu.edu/icons.gif/foot_motif.gif)
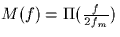 , sketch the magnitude spectrum of the signal x2(t).
, sketch the magnitude spectrum of the signal x2(t).
- 6.
- Assuming that the lowpass is ideal with cut-off frequency fm,
find an expression for the ouput signal y(t) in terms of m(t).
What effect does the phase-offset have on the non-coherent demodulator?
Hint: The following identities may be useful
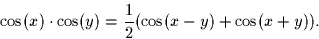
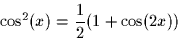



Next: Binary Signal Sets
Up: Collected Problems
Previous: Reconstruction of Sampled Signals
Prof. Bernd-Peter Paris
3/3/1998
![]() is not equal to zero, i.e.,
is not equal to zero, i.e.,
![]()
![\begin{picture}
(65,30)
\setlength {\unitlength}{1mm}
\put( 0, 20){\vector(...
...){$\times$}}
\put( 15, 5){\makebox( 0, 0)[t]{$\cos(2 \pi f_c t)$}}\end{picture}](img9.gif)
![\begin{picture}
(90,12)(0,9)
\setlength {\unitlength}{1.5mm}
\put(0,10){\ma...
...ut(70,15){\vector(1,0){10}}
\put(81,10){\makebox(9,10)[l]{$y(t)$}}\end{picture}](img11.gif)
![]()
![]()