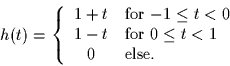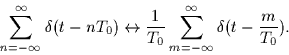Reconstruction of Sampled Signals

Consider the system shown in the following block diagram:

The impulse response h(t) of the filter in the system is given by

$$h(t) = \left\{ \begin{array} {cl} 1 + t & \mbox{for $-1 \le... ...\mbox{for $0 \leq t < 1$}\\ 0 & \mbox{else.}\end{array}\right.$$

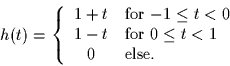
1.

For a ``typical'' low-pass signal x(t), sketch both the sampled signal y(t) and the reconstructed signal z(t).

2.

Describe in your own words

• how the signal is reconstructed from the samples and
• which conditions must hold so that the reconstructed signal z(t) approximates the input signal x(t) well.

3.

Show that the following is a Fourier transform pair

$$\sum_{n=-\infty}^{\infty} \delta(t-nT_0) \leftrightarrow \frac{1}{T_0} \sum_{m=-\infty}^{\infty} \delta(t-\frac{m}{T_0}).$$

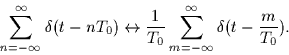
4.

Use the result from part (c) to find the Fourier transform Y(f) of the sampled signal y(t) in terms of the Fourier transform X(f) of the input signal x(t).

5.

Show that h(t) is obtained as the result of convolving a rectangular pulse 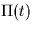$\Pi(t)$ with itself. Then, find the Fourier transform H(f) of h(t).

6.

Combine the results from parts (d) and (e) to determine the Fourier transform Z(f) of the reconstructed signal z(t). Assuming a ``typical'' spectrum for X(f) (with X(f)=0 for |f| > f_M), sketch the magnitude of Z(f). What relationship between f_M and T₀ will lead to a good reconstruction of the input signal?