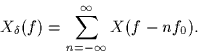Next: Multi-Path Channels Up: Collected Problems Previous: Signal Energy

Sampling Systems

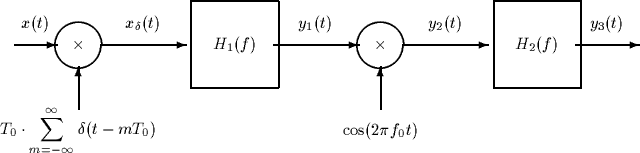
Consider a bandlimited signal x(t) with Fourier transform X(f). (X(f) = 0 for |f| > f_s.) This signal is input to the following system:

$\begin{picture} (580,130)(20,680) \setlength {\unitlength}{0.009in} % \thickl... ...lta(t-mT_0)}$}} \put(340,660){\makebox(40,40){$\cos(2 \pi f_0 t)$}}\end{picture}$

The frequency response H₁(f) of the linear system in the block diagram above is given by:

$\begin{picture} (401,172)(80,660) \setlength {\unitlength}{0.013in} % \thick... ...put(295,820){\makebox(0,0)[lb]{\raisebox{0pt}[0pt][0pt]{$H_1(f)$}}}\end{picture}$

The sampling rate 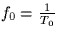$f_0 = \frac{1}{T_0}$ , the highest signal frequenct f_s, and the center frequency f_b of the band-pass H₁ are related through

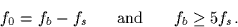
$\begin{displaymath} f_0 = f_b - f_s \mbox{\hspace*{0.2in} and \hspace*{0.2in}} f_b \geq 5f_s.\end{displaymath}$

1.: Show that the Fourier transform 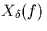$X_{\delta}(f)$ of the sampled signal 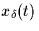$x_{\delta}(t)$ is given by
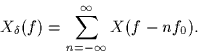
$\begin{displaymath} X_{\delta}(f) = \sum_{n=-\infty}^\infty X(f-nf_0).\end{displaymath}$
Sketch 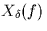$X_{\delta}(f)$ for a typical X(f).
2.: Compute the Fourier transform Y₁(f) of the output y₁(t) of the bandpass H₁. Sketch Y₁(f) for a typical X(f).
3.: Compute the Fourier transform Y₂(f) of the signal y₂(t). Sketch Y₂(f) for a typical X(f).
4.: How would you choose the frequency response of the system H₂(f) so that the overall system (between x(t) and y₃(t)) does not introduce distortion?

Prof. Bernd-Peter Paris
3/3/1998